Gọi F là trung điểm cạnh AD có
A B / / E F ⇒ A B , E C = E F , E C
Tam giác ∆ E F C có
c o s ∠ F E C = E F 2 + E C 2 - F C 2 2 . E F . E C
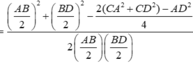
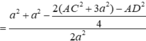
![]()
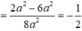
Vậy góc giữa hai đường thẳng AB và EC bằng 60 °
Chọn đáp án D.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Gọi F là trung điểm cạnh AD có
A B / / E F ⇒ A B , E C = E F , E C

Tam giác ∆ E F C có
c o s ∠ F E C = E F 2 + E C 2 - F C 2 2 . E F . E C
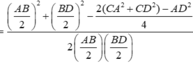
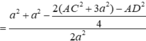
![]()
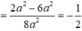
Vậy góc giữa hai đường thẳng AB và EC bằng 60 °
Chọn đáp án D.
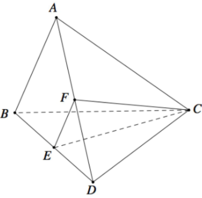
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và A B = a 6 2 ; A C = a 2 ; C D = a Gọi E là trung điểm của AD (tham khảo hình vẽ). Góc giữa hai đường thẳng AB và CE bằng
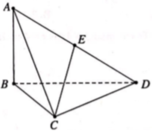
A. 60 độ
B. 45 độ
C. 30 độ
D. 90 độ
Tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng B C D , A B = 2 a . M là trung điểm của AD, gọi φ là góc giữa đường thẳng CM với mp(BCD), khi đó:
A. tan φ = 3 2
B. tan φ = 2 3 3
C. tan φ = 3 2 2
D. tan φ = 6 3
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và AB = a 6 2 ; AC = a 2 ; CD = a . Gọi E là trung tâm của AC (tham khảo hình vẽ bên). Góc giữa đường thẳng AB và DE bằng
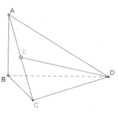
A. 45 °
B. 60 °
C. 30 °
D. 90 °
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; AB = BC = a; AD = 2a; S A ⊥ A B C D . Góc giữa mặt phẳng ( SCD ) và ( ABCD ) bằng 45 o . Gọi M là trung điểm AD. Tính theo a thể tích V khối chóp S.MCD và khoảng cách d giữa hai đường thẳng SM và BD
A. V = a 3 2 6 d = a 22 11
B. V = a 3 6 6 d = a 22 11
C. V = a 3 2 6 d = a 22 22
D. V = a 3 6 6 d = a 22 22
Cho tam giác ABC vuông tại A có AB= 9cm ; BC=10cm
a. Tính AC và so sánh các góc tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm BD. Chứng minh tam giác BCD cân
c. Gọi E; F lần lượt là trung điểm các cạnh DC, BC. Đường thẳng BE cắt cạnh AC tại M.
Tính CM và chứng minh 3 điểm D; M; F thẳng hàng
Cho hình lăng trụ đứng ABC. A 'B 'C ' có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm của AB. Cho biết A B = 2 a ; B C = 13 ; C C ' = 4 a . Khoảng cách giữa hai đường thẳng A 'B và CE bằng
A. 4 a 7
B. 12 a 7
C. 6 a 7
D. 3 a 7
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 3
D. 2 a 5 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 ° . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD)nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC
A. a 5 5
B. 5 a 3 3
C. 2 a 15 5
D. 2 a 5 5
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=a,OC=2a. Gọi M là trung điểm cạnh BC. Côsin góc giữa hai đường thẳng AB và OM bằng
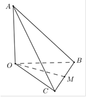
A. 10 10
B. 10 5
C. 3 10 10
D. 15 5