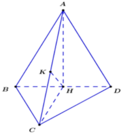
Ta có:

Xét ∆ A H C vuông tại H có đường cao KH ta có:
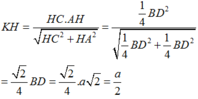
Chọn B.

Ta có:

Xét ∆ A H C vuông tại H có đường cao KH ta có:
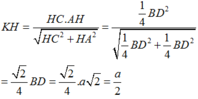
Chọn B.
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho khối hộp ABCD.A′B′C′D′ có tất cả các cạnh bằng 1. Các góc tại đỉnh A bằng 60 ° . Khoảng cách giữa hai đường thẳng BD và AC′ bằng
A. 6 6
B. 2 6
C. 3 6
D. 3 12
Cho tứ diện ABCD có AB=CD=a, AC=BD=b, AD=BC=c. Khoảng cách giữa hai đường thẳng AB và CD là
A. 1 2 b 2 + c 2 - a 2
B. 1 2 b 2 + c 2 + a 2
C. 1 4 b 2 + c 2 - a 2
D. 1 4 b 2 + c 2 + a 2
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng BD và A′C′ bằng
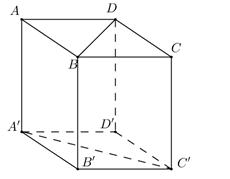
A. 2 a.
B. a.
C. 3 a.
D. 2 a 2
Cho hàm số y = 2 x − 1 x + 1 có đồ thì (C) và đường thẳng d : y = 2 x − 3. Đường thẳng d cắt (C) tại hai điểm A và B. Khoảng cách giữa A và B là
A. A B = 2 5 5
B. A B = 5 2
C. A B = 5 5 2
D. A B = 2 5
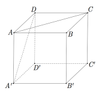
hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng AC và A′D bằng
A. 2 2 a
B. 3 3 a
C. 3 6 a
D. 2 3 a
Cho khối lăng trụ tứ giác đều ABCD. A 'B 'C 'D ' có khoảng cách giữa AB và A’D bằng 2, đường chéo của mặt bên bằng 5. Biết A ' A > A D . Thể tích lăng trụ là
A. V = 30 5
B. V = 10 5 3
C. 10 5
D. 5 5
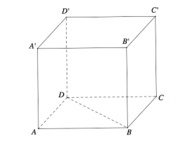
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CC′ bằng
A. a/2.
B. a 2 4
C. a 2 2
D. a/4.