Điều kiện GM = GN mới chứng tỏ điểm G nằm trên mặt phẳng trung trực của đoạn thẳng MN.
Đáp án A
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp với P là điểm bất kỳ
Đọc tiếp
Cho tứ diện ABCD các điểm M, N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm tứ diện ABCD trong trường hợp
với P là điểm bất kỳ
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Vecto M N → bằng:
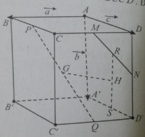
A. 1 2 c → - a →
B. 1 2 c → - b →
C. 1 2 b → - a →
D. 1 2 a → - b →
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A
B
→
+
A
C
→
+
A
D
→
bằng: A.
4
A
G...
Đọc tiếp
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
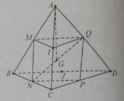
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Đường thẳng GG’ song song với mặt phẳng (AA’B’B) vì:
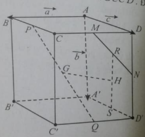
A. Vecto G G ' → cùng phương với vecto C D →
B. Vecto G G ' → cùng phương với vecto M N →
C. Vecto G G ' → đồng phẳng với hai vecto a → v à b →
D. Vecto G G ' → đồng phẳng với hai vecto b → v à c → .
25 tháng 3 2023 lúc 13:57
Cho tứ diện ABCD. Gọi G là trọng tâm của ΔBCD. Hai điểm M và N lần lượt thuộc cạnh BC,CD sao cho \(\dfrac{BM}{BC}=\dfrac{1}{4};\dfrac{NC}{ND}=\dfrac{3}{2}\). Chứng minh A,M,N,G đồng phẳng
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, BD,CD.
a. Xác định giao tuyến của hai mặt phẳng (AMN) và (ACD).
b. Chứng minh rằng đường thẳng BC song song với mặt phẳng (ANP)
c. Gọi G, H lần lượt là trọng tâm của tam giác ABC và ACD. Chứng minh GH // BD.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm
∆
BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là: A. điểm C B. điểm N C. giao điểm của đường thẳng MG và đường thẳng AN D. giao điểm của đường thẳng MG và đường thẳng BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm ∆ BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là:
A. điểm C
B. điểm N
C. giao điểm của đường thẳng MG và đường thẳng AN
D. giao điểm của đường thẳng MG và đường thẳng BC
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
Cho tứ diện ABCD có E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mp (ACD) là
A. điểm F
B. giao điểm của EG và AF
C. Giao điểm của EG và AC
D. giao điểm của EG và CD