Chọn B.
Ta có: 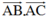 = AB. AC.cos BAC
= AB. AC.cos BAC
Mà: 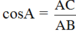
Suy ra: 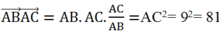
Chọn B.
Ta có: 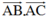 = AB. AC.cos BAC
= AB. AC.cos BAC
Mà: 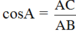
Suy ra: 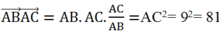
Cho tam giác ABC vuông tại A có góc B = 600, AB = a Tính A C → . C B →
A. 3a2
B. -3a2
C. a2
D. -2a2
Cho tam giác ABC vuông tại A và có AC = b; AB = c. Tính B A → . B C →
A. B A → . B C → = b 2 .
B. B A → . B C → = c 2 .
C. B A → . B C → = b 2 + c 2 .
D. B A → . B C → = b 2 − c 2 .
Cho tam giác ABC vuông tại C có AC = 9; BC = 5. Tính A B → . A C →
A. -27
B. 81
C. 9
D. -18
Cho Tam giác ABC vuông cân tại A có AB =a. Tính véctơ AB -véctơ CB ,véctơ AB + véctơ AC
Cho tam giác ABC vuông cân tại A có AB=AC=a. tính véc tơ AB, véc tơ AC; véc tơ AC, véc tơ CB
Cho điểm A(-1;1) B(3;2) C(-1/2;1)
a)Chứng minh :3điểm A B C không thẳng hàng. Tính chu vi tam giác ABC
b)Chứng minh :Tam giác ABC vuông. Tìm tâm đường tròn ngoại tiếp tam giác ABC c)Tìm D thuộc OY.Tam giác ABC vuông tại D
d)Tìm M sao cho MA^2+MB^2+MO^2 nhỏ nhất
cho tam giác ABC có A(-1;1) ; B(1;3) ; C(1;-1)
a , tam gisc ABC là tam giác gì , tính chu vi và diện tích .
b , tìm tọa độ tâm I và tính bán kính đường tròn ngoại tiếp tam giác ABC
c , tìm tọa độ điểm D có hoành độ âm sao cho tam giác ADC vuông cân tại D .
Cho ΔABC vuông tại A, biết (AB) ⃗.(CB) ⃗=4, (AC) ⃗.(BC) ⃗=9. Khi đó AB, AC, BC có độ dài là
A. 2; 3; √13. B. 3; 4; 5. C. 2; 4; 2√5. D. 4; 6; 2√13.
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8).
a Tính . Cm tam giác ABC vuông tại A.
b Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
c Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.
d Tính chu vi, diện tích tam giác ABC.
e Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.
f Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.
g Tìm toạ độ điểm D để ABDC là hình chữ nhật.
h Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.