Các câu hỏi tương tự
Cho tam giác ABC có AB c; BC a; AC b . Nếu giữa a; b; c có liên hệ b2 + c2 2a2 thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng: A.
a
3
2
B.
a
3
3
C. a D. 2a
Đọc tiếp
Cho tam giác ABC có AB = c; BC = a; AC = b . Nếu giữa a; b; c có liên hệ b2 + c2 = 2a2 thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng:
A. a 3 2
B. a 3 3
C. a
D. 2a
Trong các mệnh đề sau a. Nếu tam giác ABC thỏa mãn AB2 + AC2 BC2 thì tam giác ABC vuông tại B. b. Nếu một phương trình bậc hai có biệt thức không âm thì nó có nghiệm. c. Tam giác ABC là tam giác đều khi và chỉ khi nó thỏa mãn đồng thời hai điều kiện AB AC và góc A 600. d. Hình thang cân có một trục đối xứng. Các mệnh đề đúng là: A. a, c. B. a, b, c. C. b, c. D. b, c, d.
Đọc tiếp
Trong các mệnh đề sau
a. Nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại B.
b. Nếu một phương trình bậc hai có biệt thức không âm thì nó có nghiệm.
c. Tam giác ABC là tam giác đều khi và chỉ khi nó thỏa mãn đồng thời hai điều kiện AB = AC và góc A = 600.
d. Hình thang cân có một trục đối xứng.
Các mệnh đề đúng là:
A. a, c.
B. a, b, c.
C. b, c.
D. b, c, d.
Trong một mặt phẳng oxy cho A (4;6) b (1;4) c (7; 3/2) A. Chứng minh tam giác ABC vuông tại a B. Tính độ dài cạnh ab Có. Tính góc giữa hai vectơ a' b' biết a = (1;2) b (1;3)
Tam giác ABC vuông tại A có đường cao AH h và có BC a, CA b, AB c. Gọi BH c’ và CH b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:a2 b2 + (.....)b2 a x (.....)c2 a x (.....)h2 b’ x (.....)ah b x (.....)
Đọc tiếp
Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
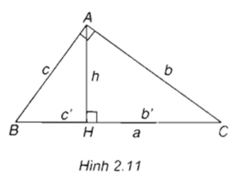
a2 = b2 + (.....)
b2 = a x (.....)
c2 = a x (.....)
h2 = b’ x (.....)
ah = b x (.....)
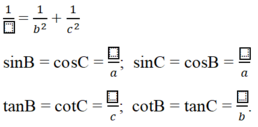
Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
A. 300
B. 600
C. 900
D. 1200
Cho tam giác ABC vuông tại A và có AC b; AB c. Tính
B
A
→
.
B
C
→
A.
B
A
→
.
B
C
→
b
2
.
B.
B...
Đọc tiếp
Cho tam giác ABC vuông tại A và có AC = b; AB = c. Tính B A → . B C →
A. B A → . B C → = b 2 .
B. B A → . B C → = c 2 .
C. B A → . B C → = b 2 + c 2 .
D. B A → . B C → = b 2 − c 2 .
Cho tam giác ABC có AB=6cm, AC=8cm và góc A=600 .Gọi M là trung điểm của BC. Qua B kẻ một đường thẳng vuông góc với AM cắt AC tại N. Tính tỉ số \(\dfrac{AN}{AC}\)
Cho Tam giác ABC a 7 b 9 c 10 Tính góc A góc B góc C diện tích Tam giác AB C
Xem chi tiết
Cho tam giác ABC có BC=a,AB=c,AC=b và diện tích S=1/4(a+b−c)(a−b+c). Tính góc A