Các câu hỏi tương tự
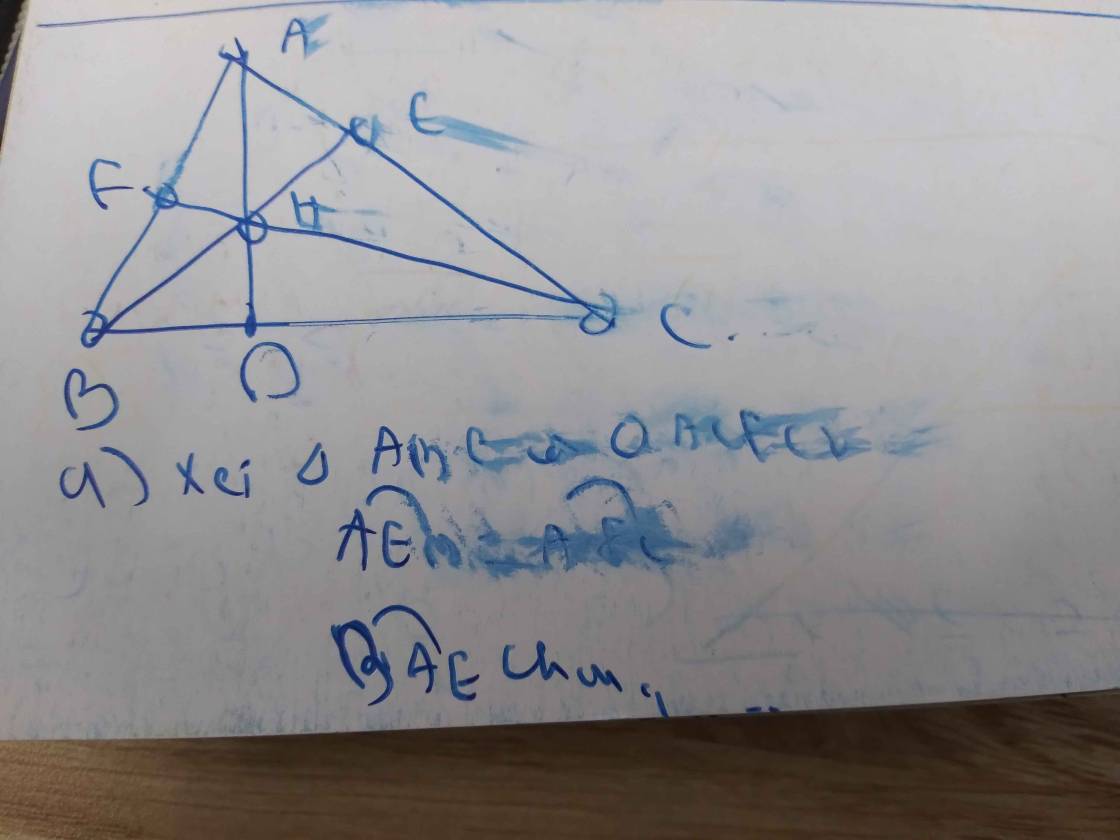
cho tam giác ABC có ba góc nhọn (ABAC), có 2 đường cao BE,CF cắt nhau tại H. a/ chứng minh tam giác ABE đồng dạng tam giác ACF. b/ chứng minh AB.AFAC.AE c/ gọi O là trung điểm BC, I là trung điểm AH. Chứng minh OI vuông góc EF. d/ Gọi M là giao điểm của OI vè EF. cho biết BAC60. Tính tỉ số AM/AO
Đọc tiếp
cho tam giác ABC có ba góc nhọn (AB<AC), có 2 đường cao BE,CF cắt nhau tại H. a/ chứng minh tam giác ABE đồng dạng tam giác ACF. b/ chứng minh AB.AF=AC.AE c/ gọi O là trung điểm BC, I là trung điểm AH. Chứng minh OI vuông góc EF. d/ Gọi M là giao điểm của OI vè EF. cho biết BAC=60. Tính tỉ số AM/AO
Cho tam giác nhọn ABC có ba đường cao AD,BE và CF cắt nhau tại H.
a) Chứng minh: Tam giác ABE đồng dạng với tám giác ACF, từ đó suy ra : AB.AF = AC.AE
b) Chứng minh: DB.DC = DA.DH
c) Gọi I là trung điểm của BC. Đường thẳng vuông góc với IH tại H cắt AB và AC lần lượt tại M và N. Chứng minh: Tam giác AHN đồng dạng với tam giác BIH và H là trung điểm của MN.
Cho tam giác ABC nhọn có AB > AC. Các đường cao AD,BE, CF cắt tại H.
a) chứng minh rằng ∆AFH~∆ADB
b) ∆ AFE~∆ABC và EH là tia phân giác của góc FED
c) gọi I là trung điểm của BC qua H kẻ đường thẳng vuông góc với HI đường thẳng này cắt AB tại M, cắt AC tại N . Chứng minh ∆ IMN cân
Cho tam giác ABC ( ABAC) nhọn, các đường cao AD,BE,CF cắt nhau tại Ha) Chứng minh tam giác AEB và tam giác AFC đồng dạng. Từ đó suy ra AF.ABAE.ACb) Chứng minh tam giác AEF và tam giác ABC đồng dạng c) Gọi K là giao điểm của của EF và BC. Gọi O là trung điểm của BC. Chứng minh rằng KF.KEKB.KC và KF.KEKO2 -BC2/4d) Tia phân giác góc BKF cắt AB tại N và tia phân giác góc BAC cắt BC tại M. chứng minh MN vuông góc ABP/s: Các bạn giải giúp mình bài trên nhé.
Đọc tiếp
Cho tam giác ABC ( AB<AC) nhọn, các đường cao AD,BE,CF cắt nhau tại H
a) Chứng minh tam giác AEB và tam giác AFC đồng dạng. Từ đó suy ra AF.AB=AE.AC
b) Chứng minh tam giác AEF và tam giác ABC đồng dạng
c) Gọi K là giao điểm của của EF và BC. Gọi O là trung điểm của BC. Chứng minh rằng KF.KE=KB.KC và KF.KE=KO2 -BC2/4
d) Tia phân giác góc BKF cắt AB tại N và tia phân giác góc BAC cắt BC tại M. chứng minh MN vuông góc AB
P/s: Các bạn giải giúp mình bài trên nhé.
Bài 4. Cho tam giác ABC với trực tâm H, trọng tâm G, tâm đường tròn ngoại tiếp O. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh rằng tam giác MON đồng dạng AHB. Từ đó chứng minh H, G, O thẳng hàng.Bài 5. Cho tam giác ABC. Dựng ra ngoài các tam giác ABF và ACE lần lượt vuông tại B, C và đồng dạng với nhau. BE giao CF tại K. Chứng minh rằng AK ⊥ BC.Bài 6. Cho tứ giác ABCD có hai đường chéo cắt nhau tại I thỏa mãn tam giác AID đòng dạng tam giác BIC. Kẻ IH ⊥ AD, IK ⊥ BC. M, N lần lượt là t...
Đọc tiếp
Bài 4. Cho tam giác ABC với trực tâm H, trọng tâm G, tâm đường tròn ngoại tiếp O. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh rằng tam giác MON đồng dạng AHB. Từ đó chứng minh H, G, O thẳng hàng.
Bài 5. Cho tam giác ABC. Dựng ra ngoài các tam giác ABF và ACE lần lượt vuông tại B, C và đồng dạng với nhau. BE giao CF tại K. Chứng minh rằng AK ⊥ BC.
Bài 6. Cho tứ giác ABCD có hai đường chéo cắt nhau tại I thỏa mãn tam giác AID đòng dạng tam giác BIC. Kẻ IH ⊥ AD, IK ⊥ BC. M, N lần lượt là trung điểm AB, CD. Chứng minh rằng MN ⊥ HK.
Bài 7. Cho tứ giác ABCD có hai đường chéo cắt nhau tại O. Gọi M, N lần lượt là trung điểm AB, CD; H, K lần lượt là trực tâm các tam giác AOD, BOC. Chứng minh rằng MN ⊥ HK.
Bài 8. Cho tam giác ABC. Các đường cao AD, BE, CF . M thuộc tia DF , N thuộc tia DE sao cho ∠M AN = ∠BAC. Chứng minh rằng A là tâm đường tròn bàng tiếp góc D của tam giác DMN .
Bài 9. Cho tứ giác ABCD có hai đường chéo AC = BD. Về phía ngoài tứ giác dựng các tam giác cân đồng dạng AMB và CND (cân tại M, N ). Gọi P, Q lần lượt là trung điểm của AD, BC. Chứng minh rằng M N vuông góc với PQ.
Bài 10. Cho tam giác ABC. Các đường cao AD, BE, CF . Trên AB, AC lấy các điểm K, L sao cho ∠FDK = ∠EDL = 90◦. Gọi M là trung điểm KL. Chứng minh rằng AM ⊥ EF .
Mong các bạn giúp đỡ mình. Giúp được bài nào thì giúp nhé.
Cho tam giác ABC có 3 góc nhọn. Ba đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: tam giác AEB đồng dạng với tam giác AFC. Tính tỉ số đồng dạng với AB=4cm, AC=6cm.
b) Chứng minh: tam giác AEF đồng dạng với tam giác ABC.
c) Kéo dài EF và BC cắt nhau tại I. Gọi M là trung điểm của BC. Chứng minh: IE.IF=IM^2-BC^2/4.
d) Gọi N là trung điểm của AH. Chứng minh: MN vuông góc với EF.
Bài 23 : Cho tam giác ABC vuông tại A ( AB AC ) . Gọi F là trung điểm của BC , qua F kẻ đường thẳng d vuông góc và BC , đường thẳng d cắt đường thẳng AB , AC lần lượt tại D và E. a ) Chứng minh : tam giác AED đồng dạng với tam giác PEC b ) Chứng minh , BF.FC DF.EF c ) Tính BC biết DE 5cm , EF 4cm . d ) Gọi K là giao điểm của BE và DC , đường thẳng FK cắt AC tại I. Chứng minh : AC. EI AE . IC .Bài 26 : Cho tam giác ABC vuông tại A , đường cao AH . Gọi E , F lần lượt là chân đường vuông g...
Đọc tiếp
Bài 23 : Cho tam giác ABC vuông tại A ( AB < AC ) . Gọi F là trung điểm của BC , qua F kẻ đường thẳng d vuông góc và BC , đường thẳng d cắt đường thẳng AB , AC lần lượt tại D và E.
a ) Chứng minh : tam giác AED đồng dạng với tam giác PEC
b ) Chứng minh , BF.FC = DF.EF
c ) Tính BC biết DE = 5cm , EF = 4cm
. d ) Gọi K là giao điểm của BE và DC , đường thẳng FK cắt AC tại I. Chứng minh : AC. EI = AE . IC
.Bài 26 : Cho tam giác ABC vuông tại A , đường cao AH . Gọi E , F lần lượt là chân đường vuông góc kẻ tử H đến AB , AC
a ) Chứng minh : AH = EF
b ) Chứng minh : AB^2 = BH.BC
c ) Chứng minh :tam giác HEF đồng dạng vớ itam giác ABC
d ) Kẻ tìa Bx vuông góc BC , Bx cắt đường thẳng AC tại K. Gọi O là giao điểm của EF và AH . Chứng minh : CO đi qua trung điểm của KB .
Bài 27 : Cho tam giác ABC có góc A = 90 độ ; AB = 15cm , AC = 20cm , đường phân giác BD cắt đường cao AH tại K.
a ) Tính BC , AD
b ) Chứng minh tam giác AHB đồng dạng với tam giác CAB ,
c ) Chứng minh : BH.BD = BK.BA , d ) Gọi M là trung điểm của KD . Kẻ tia Bx song song với AM . Tia Bx cắt tia AH tại J , Chứng minh : HK.AJ = AK.HJ .
Cho tam giác nhọn ABC có AB < AC. Ba đường cao AD, BE và CF cắt nhau tại H. AH cắt EF tại I.
a/ Chứng minh tam giác ABE và ACF đồng dạng, tam giác AEF và ABC đồng dạng.
b/ Vẽ FK vuông góc BC tại K. Chứng minh AC.AE = AH.AD và CH.DK = CD.HF.
c/ Chứng minh EI/ED = HI/HD.
d/ Gọi M, N lần lượt là trung điểm của AF và CD. Chứng minh tổng các góc BME và BNE bằng 180o.
Cho tam giác ABC nhọn (AB AC), 3 đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: tam giác ABE đồng dạng ACF từ đó suy ra AB.AFAC.AE
b) Chứng minh: AFE ACB
c) Đường thẳng EF cắt AD và tia CB lần lượt tại I và K. Chứng minh: KF. IE KE . IF
Mong các bạn giúp mình :D
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC), 3 đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: tam giác ABE đồng dạng ACF từ đó suy ra AB.AF=AC.AE
b) Chứng minh: AFE = ACB
c) Đường thẳng EF cắt AD và tia CB lần lượt tại I và K. Chứng minh: KF. IE = KE . IF
Mong các bạn giúp mình :D