Do tam giác ABC là tam giác nên A C B ^ = 60 o
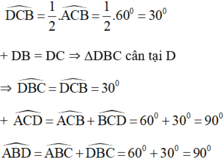
=> Tứ giác ABDC có: ![]()
=> ABDC là tứ giác nội tiếp

Do tam giác ABC là tam giác nên A C B ^ = 60 o
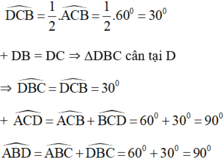
=> Tứ giác ABDC có: ![]()
=> ABDC là tứ giác nội tiếp
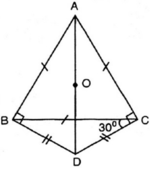
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và DCB ^ = 1 2 ACB ^
a) Chứng minh tứ giác ABDC là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, D, C.
Cho tam giác ABC có đáy BC và góc A = 20 ° .Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và góc (DAB) = 40 ° .Gọi E là giao điểm của AB và CD. Chứng minh ACBD là một tứ giác nội tiếp
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và D C B ^ = 1 2 A C B ^ . Xác định tâm của đường tròn đi qua bốn điểm A, B, D, C
Cho tam giác đều ABC. Trên tia đối của tia CB lấy điểm D sao cho BC>CD. Vẽ tam giác đều CED thuộc nửa mặt phẳng bờ BC chứa A. Gọi M,N,I,J lần lượt là trung điểm của các đoạn thẳng AC,AD,EC,BE. Chứng minh: a) Tứ giác MNIJ là hình thang cân b) JN=AE/2
Cho tam giác ABC có đáy BC và ^A=20độ.Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA=DB và ^DAB=40 độ.Gọi E là giao điểm của AB và CD .
a) CMR ABCD nội tiếp đường tròn
b) Tính ^AED
Cho tam giác ABC và M là trung điểm BC. Tiếp tuyến tại B của đường tròn ngoại tiếp tam giác ABM cắt tiếp tuyên tại điểm C của đường tròn ngoại tiếp tam giác ACM tại D.
a) Chứng minh tứ giác ABDC là tứ giác nội tiếp
b) Gọi K là giao điểm của tia Am với đường tròn ngoại tiếp tứ giác ABDC. Chứng minh KD // BC
c) Gọi E là điểm đối xứng với D qua BC. Chứng minh M,A,E thẳng hàng
Cho tam giác nhọn ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho DA = DC, \(\widehat{ACD}=\frac{1}{2}\widehat{ABC}\)
a. CM tg ABCD nội tiếp
b. Trên đường tròn ngoại tiếp tg ABCD, lấy E,F theo thứ tự là các điểm chính giữa của các cung bị chắn CB, BA bởi các góc CAB, góc BCA. Chứng minh BD vuông góc EF.
c. Gọi M là giao điểm BD và CF. CMR tam giác CDM cân.
Cho tam giác ABC nhọn (AB < AC) nội tiếp (O; R), các đường cao BD, CE cắt nhau tạiH. AH cắt BC, DE lần lượt tại F và K.
a) Chứng minh rằng tứ giác ADHE nội tiếp đường tròn, xác định tâm I của đường tròn này.
b) Vẽ tia Cx là tiếp tuyến của (O) (tia Cx nằm trên nửa mặt phẳng bờ BC không chứa điểmA). Chứng minh rằng tứ giác ADFB nội tiếp đường tròn và Cx // DF.
c) Chứng minh rằng DH là tia phân giác của góc EDF và AF.HK = AK.HF.
d) Chứng minh tam giác FBK đồng dạng tam giác FIC rồi suy ra K là trực tâm tam giác BIC
*Sửa giúp em câu c & d ạ
Cho đường tròn (O) và đường thẳng d không giao với (O). Kẻ OH vuông góc với d tại H. Trên d lấy một điểm A và kẻ tiếp tuyến AB với (O) ( B là tiếp điểm) sao cho A và B nằm cùng nửa mặt phẳng bờ là đường thẳng OH. Gọi E là giao điểm của BH với (O). Chứng minh:
a/Tứ giác OBAH nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác trên.
b/ góc BOE = 2 góc AOH
c/Đặt OA = a. Tiếp tuyến của (O) tại E cắt d tại C. Tính OC theo a.