Các câu hỏi tương tự
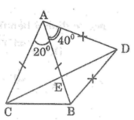
Cho tam giác ABC có đáy BC và góc A = 20 ° . Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và góc (DAB) = 40 ° .Gọi E là giao điểm của AB và CD. Tính góc (AED)
Cho tam giác ABC có đáy BC và ^A=20độ.Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA=DB và ^DAB=40 độ.Gọi E là giao điểm của AB và CD .
a) CMR ABCD nội tiếp đường tròn
b) Tính ^AED
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và D C B ^ = 1 2 A C B ^ . Chứng minh tứ giác ABDC là tứ giác nội tiếp.
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và DCB ^ = 1 2 ACB ^
a) Chứng minh tứ giác ABDC là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, D, C.
Cho (O). Từ M ngoài đường tròn vẽ hai tiếp tuyến MA và MB (B và A là hai tiếpđiểm). Trên nửa mặt phẳng bờ MO có chứa B vẽ cát tuyến MCD không qua O (MCMD). H là giao của MO và AB. Gọi I là trung điểm của CD.a) Chứng minh: OI vuông góc CD và tứ giác MAOI nội tiếp.b) Chứng minh: MC.MD MA2c) Chứng minh góc MHC góc DHOd) Trên cung nhỏ AD lấy điểm N sao cho DN DB. Qua C vẽ đường thẳng song song với DN cắt MN tại E, Qua C vẽ đường thẳng song song với DB cắt AB tại F. Chứng minh tam giác CEF cânGiúp...
Đọc tiếp
Cho (O). Từ M ngoài đường tròn vẽ hai tiếp tuyến MA và MB (B và A là hai tiếp
điểm). Trên nửa mặt phẳng bờ MO có chứa B vẽ cát tuyến MCD không qua O (MC<MD). H là giao của MO và AB. Gọi I là trung điểm của CD.
a) Chứng minh: OI vuông góc CD và tứ giác MAOI nội tiếp.
b) Chứng minh: MC.MD = MA2
c) Chứng minh góc MHC = góc DHO
d) Trên cung nhỏ AD lấy điểm N sao cho DN = DB. Qua C vẽ đường thẳng song song với DN cắt MN tại E, Qua C vẽ đường thẳng song song với DB cắt AB tại F. Chứng minh tam giác CEF cân
Giúp mình câu d với cả nhà ơi
Cho đường tròn (O) và đường thẳng d không giao với (O). Kẻ OH vuông góc với d tại H. Trên d lấy một điểm A và kẻ tiếp tuyến AB với (O) ( B là tiếp điểm) sao cho A và B nằm cùng nửa mặt phẳng bờ là đường thẳng OH. Gọi E là giao điểm của BH với (O). Chứng minh:a/Tứ giác OBAH nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác trên.b/ góc BOE 2 góc AOHc/Đặt OA a. Tiếp tuyến của (O) tại E cắt d tại C. Tính OC theo a.
Đọc tiếp
Cho đường tròn (O) và đường thẳng d không giao với (O). Kẻ OH vuông góc với d tại H. Trên d lấy một điểm A và kẻ tiếp tuyến AB với (O) ( B là tiếp điểm) sao cho A và B nằm cùng nửa mặt phẳng bờ là đường thẳng OH. Gọi E là giao điểm của BH với (O). Chứng minh:
a/Tứ giác OBAH nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác trên.
b/ góc BOE = 2 góc AOH
c/Đặt OA = a. Tiếp tuyến của (O) tại E cắt d tại C. Tính OC theo a.
Cho tam giác nhọn ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho DA DC, widehat{ACD}frac{1}{2}widehat{ABC}a. CM tg ABCD nội tiếpb. Trên đường tròn ngoại tiếp tg ABCD, lấy E,F theo thứ tự là các điểm chính giữa của các cung bị chắn CB, BA bởi các góc CAB, góc BCA. Chứng minh BD vuông góc EF.c. Gọi M là giao điểm BD và CF. CMR tam giác CDM cân.
Đọc tiếp
Cho tam giác nhọn ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, lấy điểm D sao cho DA = DC, \(\widehat{ACD}=\frac{1}{2}\widehat{ABC}\)
a. CM tg ABCD nội tiếp
b. Trên đường tròn ngoại tiếp tg ABCD, lấy E,F theo thứ tự là các điểm chính giữa của các cung bị chắn CB, BA bởi các góc CAB, góc BCA. Chứng minh BD vuông góc EF.
c. Gọi M là giao điểm BD và CF. CMR tam giác CDM cân.
Cho tam giác ABC có 3 góc nhọn , trung tuyến AM. Trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB vẽ đoạn thẳng AE vuông góc với AB và AEAB. Trên nửa mặt phẳng chứa điểm B bờ là đường thẳng AC vẽ đoạn thẳng AD vuông góc với AC và ADAC.a, Chứng minh: BDCEb, Trên tia đối của MA lấy N sao cho MNMA. Chứng minh tam giác ADE tam giác CANc, Gọi I là giao điểm của DE và AM. Chứng minh: (AD^2+IE^2)/(DI^2+AE^2)1
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn , trung tuyến AM. Trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB vẽ đoạn thẳng AE vuông góc với AB và AE=AB. Trên nửa mặt phẳng chứa điểm B bờ là đường thẳng AC vẽ đoạn thẳng AD vuông góc với AC và AD=AC.
a, Chứng minh: BD=CE
b, Trên tia đối của MA lấy N sao cho MN=MA. Chứng minh tam giác ADE = tam giác CAN
c, Gọi I là giao điểm của DE và AM. Chứng minh: (AD^2+IE^2)/(DI^2+AE^2)=1
Cho nửa đường tròn đường kính AB và M là một điểm thuộc nửa đường tròn (M không trùng với A, B). Vẽ các tia Ax, By vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Lấy điểm C trên đường kính AB sao cho AC AB. Qua M kẻ đường thẳng vuông góc với MC cắt Ax tại D. Đường thẳng qua C và vuông góc với CD cắt By tại E. a) Chứng minh tứ giác ACMD nội tiếp. b) Gọi I là giao điểm của AM và CD; K là giao điểm của BM và CE. Chứng minh IK // AB. c) Ch...
Đọc tiếp
Cho nửa đường tròn đường kính AB và M là một điểm thuộc nửa đường tròn (M không trùng với A, B). Vẽ các tia Ax, By vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Lấy điểm C trên đường kính AB sao cho AC < AB. Qua M kẻ đường thẳng vuông góc với MC cắt Ax tại D. Đường thẳng qua C và vuông góc với CD cắt By tại E.
a) Chứng minh tứ giác ACMD nội tiếp.
b) Gọi I là giao điểm của AM và CD; K là giao điểm của BM và CE. Chứng minh IK // AB.
c) Chứng minh ba điểm D, M, E thẳng hàng.