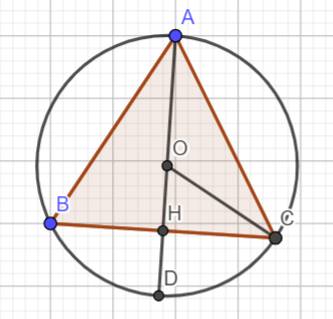
\(\Delta ABC\) đều nội tiếp (O) (gt)
\(\Rightarrow O\) là giao điểm của ba đường trung trực của \(\Delta ABC\)
\(\Rightarrow CO\) là đường trung trực của \(\Delta ABC\)
\(\Rightarrow CO\) cũng là đường phân giác của \(\Delta ABC\)
Do \(\Delta ABC\) đều (gt)
\(\Rightarrow\widehat{ACB}=60^0\)
\(\Rightarrow\widehat{ACO}=\widehat{OCH}=30^0\)
\(\Delta ABC\) đều (gt)
\(AH\) là đường cao
\(\Rightarrow AH\) cũng là đường trung trực
\(\Rightarrow A,O,H\) thẳng hàng
\(\Delta OHC\) vuông tại H
\(\Rightarrow\widehat{OCH}+\widehat{COH}=90^0\)
\(\Rightarrow\widehat{COH}=90^0-\widehat{OCH}=90^0-30^0=60^0\)
\(\Rightarrow\widehat{COD}=\widehat{COH}=60^0\)












