Chọn C.
Ta có
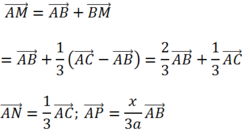
Do AM và PN vuông góc với nhau nên ![]()
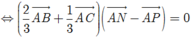
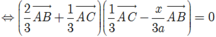
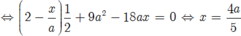
Chọn C.
Ta có
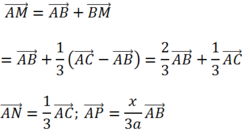
Do AM và PN vuông góc với nhau nên ![]()
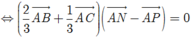
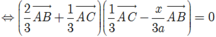
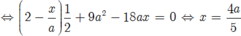
Cho \(\Delta ABC\)đều cạnh 3a. Lấy các điểm M,N,P lần lượt trên các cạnh BC,CA,AB sao cho BM=a, CN=2a, AP=x (o<x<3a
a, Biểu diễn các vecto \(\overrightarrow{AM},\overrightarrow{PN}\)theo \(\overrightarrow{AB},\overrightarrow{AC}\)
b, Tìm x để AM \(\perp\)PN
Tam giác ABC vuông tại A, có AB = AC = a. Điểm M nằm trên cạnh BC sao cho \(BM=\dfrac{BC}{3}\) . Tính độ dài AM
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
Cho tam giác ABC vuông tại A, góc B = 60. Gọi I là trung điểm cạnh BC.Trên các cạnh AB,AC lần lượt lấy các điểm M,N.Chứng minh rằng MI vuông góc với NI khi và chỉ khi BM + căn 3 CN = BC
Câu 1: Cho tam giác đều ABC có cạnh là 10a, M là trung điểm của BC. Tính | vec AB + vec AM | ? vec AM . vec BA ? Câu 2: Cho tam giác ABC vuông tại A có AB = 2a căn 3 ; AC = 2a . Tính ? vec AB . vec BC ; | vec AB - vec AC |
cho tam giác ABC có AB=5 , AC=6 , góc A = 120 độ
Gọi N là điểm thỏa mãn : vt NA + 2.vt AC = vt 0 . Gọi K là điểm trên cạnh BC sao cho vt BK = x. vt BC . Tìm x để AK vuông góc BN
Cho tam giác ABC vuông tại A có AB=3a, AC=4a, (a>0) , I là trung điểm AC. Lấy điểm M thuộc đoạn BC, đặt BC=x (0<x<5a) . Tìm x để AM vuông góc với BI
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất
Cho tam giác ABC vuông tại A có AB=3a, AC=4a, (a>0) , I là trung điểm AC. Lấy điểm M thuộc đoạn BC, đặt BC=x (0<x<5a) . Tìm x để AM vuông góc với BI