Chọn đáp án A
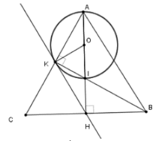
Gọi O là trung điểm AI. Xét tam giác vuông AIK có
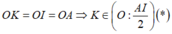
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI
Chọn đáp án A

Gọi O là trung điểm AI. Xét tam giác vuông AIK có
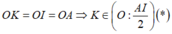
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI
Cho tam giác cân ABC tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI
A. HK
B. IB
C. IC
D. AC
Cho tam giác ABC cân tại A có các đường cao AH và BK cắt nhau tại I. Chứng minh:
a, Đường tròn đường kính AI đi qua K
b, HK là tiếp tuyến của đường tròn đường kính AI
Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau tại I. CMR: HK là tiếp tuyến của đường tròn đường kính AI.
Cho tam giác ABC cân tại , các đường cao AH bà BK cắt nhau tại I. Chứng minh HK là tiếp tuyến của đường tròn đường kính AI
Cho tam giác ABC cân Tại A đường cao AH và BK cắt nhau tại I
a) Chứng minh tam giác BKH cân tại H
b) Gọi O là trung điểm của AI .Chứng Minh góc BKH = góc IAK
c) Chứng minh HK là tiếp tuyến của đường tròn tâm O
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm A bán kính AH và kẻ thêm đường kính HD của đường tròn đó. Từ D kẻ tiếp tuyến với đường tròn, cắt AC kéo dài tại E.
a.Chứng minh rằng tam giác BEC là tam giác cân tại B.
b.Chứng minh rằng BE là tiếp tuyến của đường tròn tâm A bán kính AH.
cho tam giác abc cân tại a đường cao ah và bk bk cắt ah tại i cm hk là tiếp tuyến
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Đường cao AH cắt đường tròn tại D
a) Vì sao AD lad đường kính của đường tròn tâm O
b) Cho biết AC = 10 cm, BC = 12 cm. Tính đường cao AH và BK của đường tròn tâm O
Giải giùm mình với
Bài 1:
Cho tam giác ABC vuông tại A và có đường cao AH = 3cm. Vẽ đường tròn (A ; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn tại D cắt AC ở E.
a. Chúng minh AC = AE và tam giác BEC là tam giác cân.
b. Tính giá trị của tích BH.ED.
c. Chúng minh đường thẳng BE là tiếp tuyến của đường tròn (A ; AH).
Bài 2:
Cho đường tròn (O;R), dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O;R) tại B và C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a. Chứng minh bốn điểm A, B, O, C cùng nằm trên đường tròn.
b. Chứng minh OA vuông góc với BC.
c. Chứng minh BC là phân giác góc ABH
d. Gọi E là giao điểm AC và BD. Chứng minh tam giác EAB cân