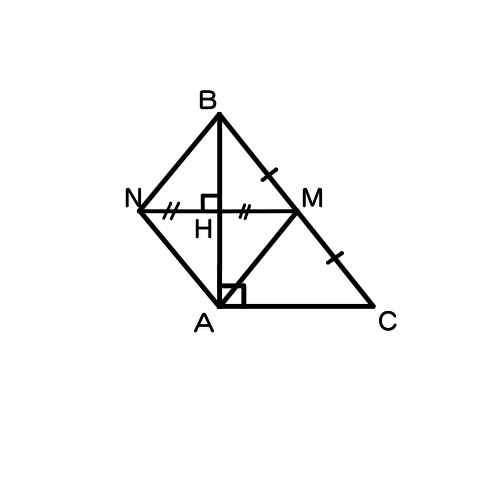
a/ - Do N đối xứng với M qua AB => AB là đường trung trực của MN hay AB ⊥ MN
- AB ⊥ AC (△ABC vuông tại A)
=> MN // AC (đpcm)
b/ Xét △HBM và △HBN :
- HB chung
- Góc BHM = Góc BHN = 90o (gt)
- HN = HM (gt)
=> △HBM = △HBN (c.g.c)
=> BN = BM
Tứ giác ANBM có BN = BM hay hai cạnh kề bằng nhau => Tứ giác ABNM là hình thoi
Vậy : HA = HB (đpcm)
- Do tứ giác ANBM là hình thoi => AN = BM
Mà BM = CM (trung tuyến AM) => AN = MC (1)
Hình thoi ANBM có AN // BM => AN // MC (2)
Từ (1) và (2), suy ra tứ giác ANMC là hình bình hành
Vậy MN = AC (đpcm)
c/ Do AN // MB (ABNM là hình thoi), AN // MC (cmt)
=> AN // BC
Vậy: Tứ giác ACBN là hình thang (đpcm).
a) Ta có: NM⊥AB(gt)
AC⊥AB(gt)
Do đó: MN//AC(Định lí 1 từ vuông góc tới song song)
b) Xét ΔABC có
M là trung điểm của BC(gt)
MH//AC(cmt)
Do đó: H là trung điểm của AB(Định lí 1 về đường trung bình của tam giác)
Suy ra: HA=HB
Xét ΔBAC có
H là trung điểm của AB(cmt)
M là trung điểm của BC(gt)
Do đó: HM là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: \(HM=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà \(HM=\dfrac{MN}{2}\)(H là trung điểm của MN)
nên AC=MN