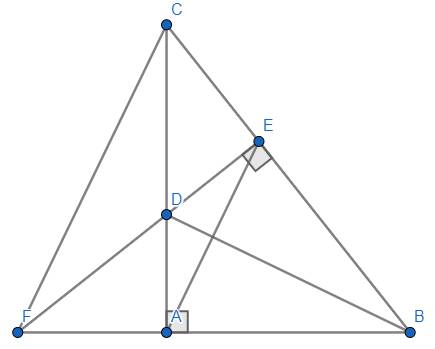
(a) Xét \(\Delta ABD,\Delta EBD:\left\{{}\begin{matrix}\hat{BAD}=\hat{BED}=90^o\left(gt\right)\\\text{BD chung}\\\hat{EBD}=\hat{ABD}\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.h-g.n\right)\Rightarrow\left\{{}\begin{matrix}BA=BE\\DA=DE\end{matrix}\right.\)
\(\Rightarrow BD\) là đường trung trực của \(AE\left(đpcm\right).\)
(b) Xét \(\Delta ADF,\Delta EDC:\left\{{}\begin{matrix}\hat{DAF}=\hat{DEC}=90^o\left(gt\right)\\AD=DE\left(cmt\right)\\\hat{ADF}=\hat{EDC}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADF=\Delta EDC\left(g.c.g\right)\Rightarrow AF=CE.\)
Lại có: \(BA=BE\left(cmt\right)\Rightarrow BA+AF=BE+CE\Leftrightarrow BC=BF\)
\(\Rightarrow\Delta BCF\) cân tại \(B.\)
Ta cũng có: \(\left\{{}\begin{matrix}FE\perp BC\\CA\perp BF\\FE\cap CA=\left\{D\right\}\end{matrix}\right.\Rightarrow BD\) là đường cao thứ ba của \(\Delta BCF\Rightarrow BD\) vừa là đường cao, vừa là đường trung trực của \(CF\Rightarrow DC=DF\left(đpcm\right).\)