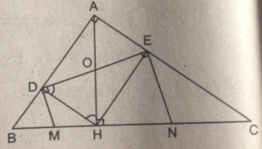
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Gọi D, E là các hình chiếu của H trên AB, AC và M, N theo thứ tự là các trung điểm của các đoạn thẳng BH, CH.
a) C/m AH = DE
b) C/m tứ giác MDEN là hthang vuông
c) Gọi P là giao điểm của đường thẳng DE với đường cao AH và Q là trung điểm của đoạn thẳng MN. C/m PQ vuông góc với DE
a: Xét tứ giác ADHE có góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
=>AH=DE
b: gó MDE=góc MDH+góc EDH
=góc MHD+góc EAH
=góc HAC+góc HCA=90 độ(1)
góc NED=góc NEH+góc DEH
=góc CHE+góc DAH
=góc HAB+góc HBA=90 độ(2)
Từ (1) và (2) suy ra NEDM là hình thang vuông
Đúng 0
Bình luận (0)
.
.
