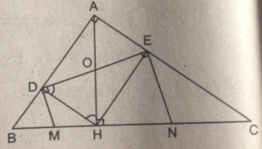
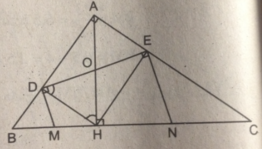
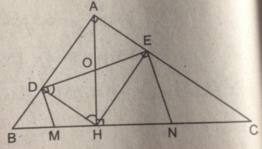
Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà 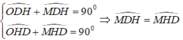
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.