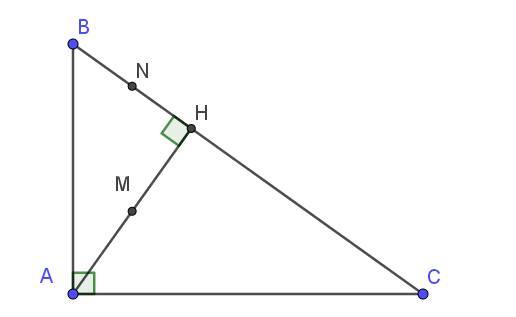
Lời giải:
Xét tam giác $BAH$ và $ACH$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{BAH}=\widehat{ACH}$ (cùng phụ với $\widehat{HAC}$)
$\Rightarrow \triangle BAH\sim \triangle ACH$ (g.g)
$\Rightarrow \frac{BH}{AH}=\frac{AH}{CH}$
$\Rightarrow AH^2=BH.CH(1)$
Mà $M,N$ là trung điểm của $AH,BH$ nên:
$AH=2HM, BH=2HN(2)$
Từ $(1); (2)$ suy ra:
$AH.2HM=2HN.CH$
$\Rightarrow AH.HM=CH.HN$
cho tam giác abc vuông tại a đường cao ah M,N lần lượt là trung điểm của AH và BH O là giao điểm của AN và CM.CMR:AN vuông góc với Cm và AH2=4MC.MO
Cho tam giác ABC vuông tại A.Kẻ đường cao AH.Gọi M,N lần lượt là trung điểm của BH và AH.Chứng minh:
a,Tam giác ABM đồng dạng tam giác CAN
b,AM vuông góc CN
cho tam giác ABC vuông tại A có đường cao AH.Gọi M,N lần lượt là hình chiếu của H lên AB,AC.
a)chứng minh HMAN là hình chữ nhật
b)Gọi O là giao điểm cũa AH và MN.I,K là trung điểm của BH và HC.CHứng minh BO vuông góc với AK
c)Chứng minh:MIKN là hình thang vuông
cho tam giác ABC vuông tại A có đường cao AH.Gọi M,N lần lượt là hình chiếu của H lên AB,AC.
a)chứng minh HMAN là hình chữ nhật
b)Gọi O là giao điểm cũa AH và MN.I,K là trung điểm của BH và HC.CHứng minh BO vuông góc với AK
c)Chứng minh:MIKN là hình thang vuông
cho tam giác ABC vuông tại A có đường cao AH.Gọi M,N lần lượt là hình chiếu của H lên AB,AC.
a)chứng minh HMAN là hình chữ nhật
b)Gọi O là giao điểm cũa AH và MN.I,K là trung điểm của BH và HC.CHứng minh BO vuông góc với AK
c)Chứng minh:MIKN là hình thang vuông
cho tam giác abc vuông tại a, đường cao ah. m, n lần lượt là trung điểm ah, bh. chứng minh mn vuông góc ac
Cho tam giác ABC vuông tại A, đường cao AH.Gọi D,E lần lượt là chân đường vuông góc kẻ từ H đến AB và AC
a)CMR AH=DE
b) Gọi i,k lần lượt là trung điểm của BH,HC.CMR DIKE là hình bình hành
c,Gọi M là trung điểm của BC .CMR AM vuông góc với DE
Cho tam giác ABC vuông tại A đường cao AH gọi M và N lần lượt là trung điểm AH và BH gọi O là giao điểm AN với CM. Chứng minh
a) AN vuông góc với CM
b) AH^2= 4MC.MO
cho tam giác abc vuông tại A. Biết Ac=12,5543 cm và trung tuyến AI=9,7786cm. Dựng đường cao AH. Gọi M,N lần lượt là trung điểm của AH, Bh gọi K là giao điểm của NM và AC. Tính góc ABC,ACB,NAK (= đơn vị đo độ) và đoạn AK (= cm )
