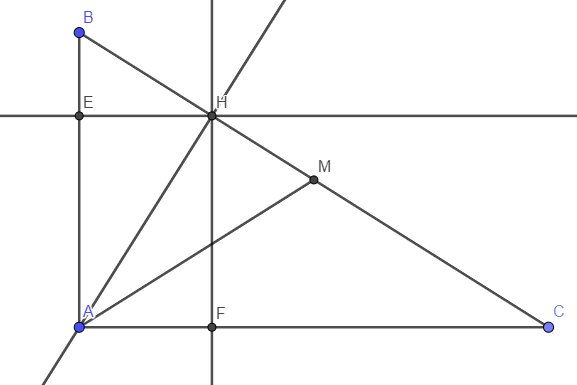
Vì \(\Delta ABC\) vuông tại A có M là trung điểm BC nên \(AM=MB=MC\)
Ta có: \(\widehat{AMB}=\widehat{MAC}+\widehat{MCA}=2.\widehat{ACB}\) (\(\Delta MAC\) cân tại M)
\(\Rightarrow\sin\widehat{AMB}=\sin2.\widehat{ACB}=2.\sin\widehat{ACB}.\cos\widehat{ACB}\)