Theo tính chất của hai tiếp tuyến cắt nhau ta có:
AB là tia phân giác của góc HAD
Vậy ba điểm D, A, E thẳng hàng.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
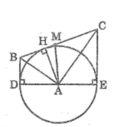
Cho tam giác ABC vuông tại, đường cao AH. Vẽ đường tròn (A; AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). Chứng minh: a) BC là tiếp tuyến của đường tròn (A; AH) b) BD = BH; CE = CH c)BD+CE=BC d) Chứng minh ba điểm D, A, E thẳng hàng HẾT.
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A: AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).
a) Chứng minh bốn điểm A, H, C, E cùng thuộc một đường tròn.
b) Chứng minh AH BD; CE và DE là tiếp tuyến đường tròn đường kính BC.
c) Kẻ đường cao HK của tam giác HDE cắt BE tại I. Chứng mình 1 là trung điểm của HK.
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A: AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).
a) Chứng minh bốn điểm A, H, C, E cùng thuộc một đường tròn.
b) Chứng minh AH = BD; CE và DE là tiếp tuyến đường tròn đường kính BC.
c) Kẻ đường cao HK của tam giác HDE cắt BE tại I. Chứng mình 1 là trung điểm của HK.
Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Đường cao AH. Vẽ đường tròn tâm A, bán kinh AH, kẻ các tiếp tuyến BD, CE với đường tròn tâm A (D. E là các tiếp điểm khác H). a) Tinh BC. AH. b) Chứng minh rằng : Ba điểm D. A. E thẳng hàng.
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A;AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).
Chứng minh rằng:
DE tiếp xúc với đường tròn các đường kính BC
Cho ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm A, bán kính AH, kẻ tiếp tuyến BD, CE với đường tròn tâm A(D,E là các tiếp điểm khác H). Chứng minh rằng:a. Ba điểm D,A,E thẳng hàng b.DE tiếp xúc với đường tròn có đường kính BC.
Đọc tiếp
Cho format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1c213877427b46fa96cff6c39e8%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%229.5%22%20y%3D%2216%22%3E%26%23x25B3%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm A, bán kính AH, kẻ tiếp tuyến BD, CE với đường tròn tâm A(D,E là các tiếp điểm khác H). Chứng minh rằng:
a. Ba điểm D,A,E thẳng hàng
b.DE tiếp xúc với đường tròn có đường kính BC.
Cho tam giác ABC đường cao AH vẽ đường tròn tâm a bán kính ah kẻ các tiếp tuyến BD CE với đường tròn be là các tiếp điểm khác chứng minh rằng a ba điểm da e thẳng hàng b d tiếp xúc với đường tròn có đường kính BC c gọi ba cắt d h tại I AC cắt he tại k chứng minh các điểm a yh k thuộc một đường tròn
Mik càn gấp
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Từ B, C kẻ các tiếp tuyến BD, CE với (A) trong đó D, E là các tiếp điểma, Chứng minh ba điểm A, D, E thẳng hàngb, Chứng minh BD.CE
D
E
2
4
c, Gọi M là trung điểm CH. Đường tròn tâm M đường kính CH cắt (Ạ) tại N với N khác H. Chứng minh CN và AM song song
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Từ B, C kẻ các tiếp tuyến BD, CE với (A) trong đó D, E là các tiếp điểm
a, Chứng minh ba điểm A, D, E thẳng hàng
b, Chứng minh BD.CE = D E 2 4
c, Gọi M là trung điểm CH. Đường tròn tâm M đường kính CH cắt (Ạ) tại N với N khác H. Chứng minh CN và AM song song
Cho Tam Giác ABC vuông tại A, đường cao AH Vẽ đường tròn Tâm A bán kính AH kẻ các tiếp tuyến BD.CE với đường tròn Tâm A (D,E lÀ các tiếp điểm khác H). Chứng minh rằng a DB + EC = BC b Ba điểm D,A,E thẳng hàng c DE tiếp súc với đường tròn có đường kính BC
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Từ B, C kẻ các tiếp tuyến BD, CE với (A) trong đó D, E là các tiếp điểma, Chứng minh ba điểm A, D, E thẳng hàngb, Chứng minh BD.CE DE24
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A; AH). Từ B, C kẻ các tiếp tuyến BD, CE với (A) trong đó D, E là các tiếp điểm
a, Chứng minh ba điểm A, D, E thẳng hàng
b, Chứng minh BD.CE =