Question

Cho tam giác ABC vuông tại A, đpg góc A cắt BC tại D, đường thẳng qua D // với AB cắt AC ở E. Cmr

a) DB/DC = AB/AC.

b) CD/CB = CE/CA = DE/AB.

c) Biết AB = 21cm, AC = 28cm. Tính DB, DC, DE.

(Mình đang cần gấp mong các bạn giúp mình.)

Answer 1

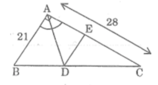
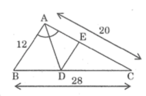
a: Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)

b: Xét ΔCAB có ED//AB

nên \(\dfrac{CD}{CB}=\dfrac{CE}{CA}=\dfrac{ED}{AB}\)

c: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=21^2+28^2=35^2\)

=>BC=35(cm)

Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{21}=\dfrac{DC}{28}\)

=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)

mà DB+DC=BC=35cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{35}{7}=5\)

=>\(DB=3\cdot5=15\left(cm\right);DC=4\cdot5=20\left(cm\right)\)

Xét ΔCAB có ED//AB

nên \(\dfrac{ED}{AB}=\dfrac{CD}{CB}\)

=>\(\dfrac{ED}{21}=\dfrac{20}{35}=\dfrac{4}{7}\)

=>\(ED=21\cdot\dfrac{4}{7}=12\left(cm\right)\)