Các câu hỏi tương tự
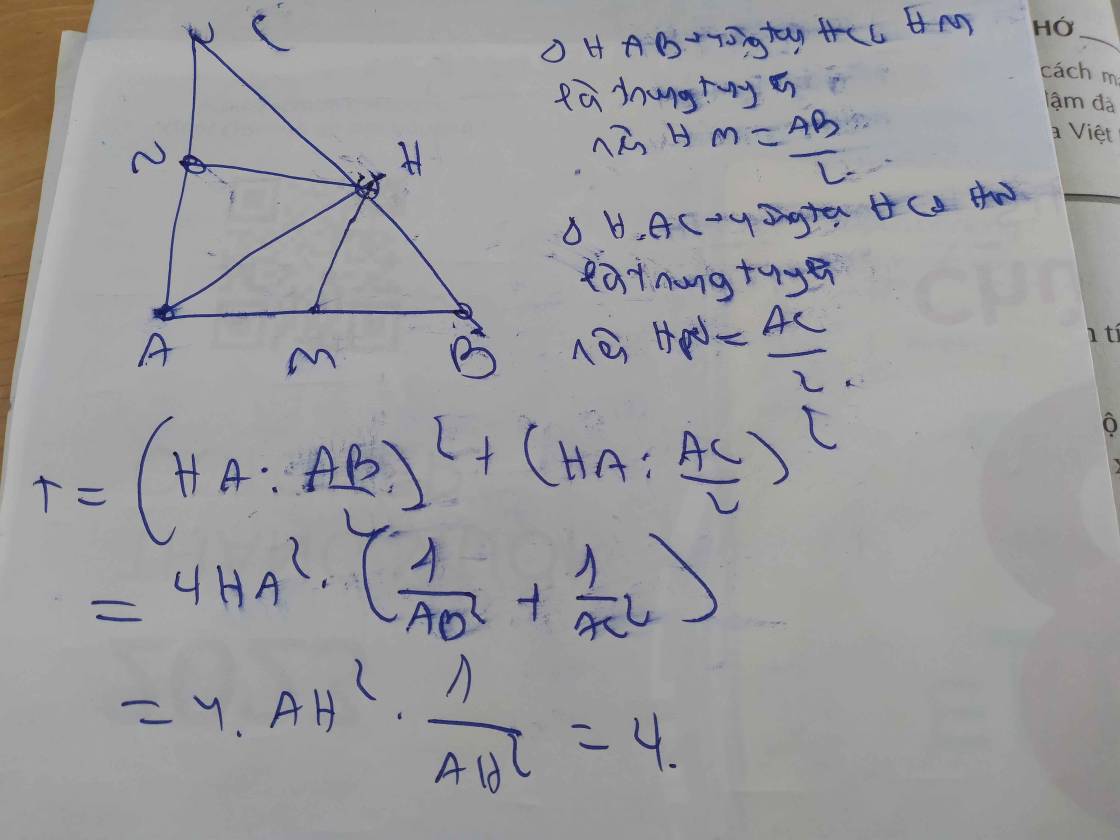
Cho tam giac ABC vuông tại A, kẻ đường cao AH gọi M,N lần lượt là trung điểm của AB và AC. CMR: HM vuông góc với HN.
Cho tâm giác ABC có đường cao AH. Gọi M,N lần lượt là trung điểm của AB, AC. Hạ BE, CF lần lượt vuông góc vs HN và HM. chứng minh 3 đường thẳng AH, BE, CF đông quy
Cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E lần lượt là hình chiếu của điểm H trên các cạnh AB và AC
a, Chứng minh AD . AB = AE . AC
b, Gọi M , N lần lượt là trung điểm của BH và CH . Chứng minh DE là tiếp tuyến chung của 2 đường tròn ( M , MD ) và ( N , NE )
c,Gọi P là trung điểm MN , Q là giao điểm của DE và AH , giả sử AB=6cm , AC=8cm . Tính độ dài PQ
Cho tam giác ABC vuông tại A(AB AC), đường cao AH. Đường tròn tâm ở đường kính AH cắt các cạnh AB, AC lần lượt tại M, N,
1) Chứng minh tứ giác AMIN là hình chữ nhật và AM AB AN AC
2) Gọi O là trung điểm của cạnh BC, D là giao điểm của MV và On
Chứng minh tứ giác BAVC nội tiếp và O L M N
3) Gọi P là giao điểm của BC và MN, K là giao điểm thứ hai của AP và đường tròn () đường kính AH. Chứng minh rằng BKC 90°
Đọc tiếp
Cho tam giác ABC vuông tại A(AB < AC), đường cao AH. Đường tròn tâm ở đường kính AH cắt các cạnh AB, AC lần lượt tại M, N, 1) Chứng minh tứ giác AMIN là hình chữ nhật và AM AB = AN AC 2) Gọi O là trung điểm của cạnh BC, D là giao điểm của MV và On Chứng minh tứ giác BAVC nội tiếp và O L M N 3) Gọi P là giao điểm của BC và MN, K là giao điểm thứ hai của AP và đường tròn () đường kính AH. Chứng minh rằng BKC 90°
cho tam giác ABC có 3 góc nhọn AB<AC, đường cao AH.Từ Ha kẻ HM và HN lần lượt vuông góc với AB và AC.
a.cm. AMHN là tứ giác nội tiếp
b. cm ˆAMN=ˆABC
c. gọi O là tâm đường tròn ngoại tiếp tam giác ABC có đường kính AD cắt MN tại K.cm AH là tiếp tuyến của đường tròn ngoại tiếp tam giác HKD.
cho tam giác ABC có 3 góc nhọn AB<AC, đường cao AH.Từ Ha kẻ HM và HN lần lượt vuông góc với AB và AC.
a.cm. AMHN là tứ giác nội tiếp
b. cm ˆAMN=ˆABC
c. gọi O là tâm đường tròn ngoại tiếp tam giác ABC có đường kính AD cắt MN tại K.cm AH là tiếp tuyến của đường tròn ngoại tiếp tam giác HKD.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N theo thứ tự là trung điểm AB, AC. Biết HM 15cm, HN 20cm. Tính HB, HC, AH A. HB 12cm; HC 28cm; AH 20cm B. HB 15cm; HC 30cm; AH 20cm C. HB 16cm; HC 30cm; AH 22cm D. HB 18cm; HC 32cm; AH 24cm
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N theo thứ tự là trung điểm AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH
A. HB = 12cm; HC = 28cm; AH = 20cm
B. HB = 15cm; HC = 30cm; AH = 20cm
C. HB = 16cm; HC = 30cm; AH = 22cm
D. HB = 18cm; HC = 32cm; AH = 24cm
cho tam giác ABC có 3 góc nhọn AB<AC, đường cao AH.Từ Ha kẻ HM và HN lần lượt vuông góc với AB và AC.
a.cm. AMHN là tứ giác nội tiếp
b. cm ^AMN=^ABC
c. gọi O là tâm đường tròn ngoại tiếp tam giác ABC có đường kính AD cắt MN tại K.cm AH là tiếp tuyến của đường tròn ngoại tiếp tam giác HKD
Cho tam giác ABC vuông tại A. Gọi I là tâm đường tròn nội tiếp tam giáo ABC, các tiếp điểm trên BC, CA, AB lần lượt là D,E,F. Gọi M là trung điểm của AC, đường thẳng MI cắt cạnh AB tại N, đường thẳng DF cắt đường cao AH của tam giác ABC tại P. Chứng minh tam giác ANP là tam giác cân.