Các câu hỏi tương tự
Cho tam giác ABC vuông tại A có BC 2a và
∠
B 30
°
. Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi
S
1
là diện tích toàn phần của hình nón đó và
S
2
là diện tích mặt cầu đường kính AB. Khi đó, tỉ số
S
1
/
S
2...
Đọc tiếp
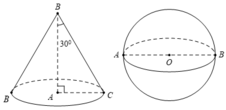
Cho tam giác ABC vuông tại A có BC = 2a và ∠ B = 30 ° . Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích toàn phần của hình nón đó và S 2 là diện tích mặt cầu đường kính AB. Khi đó, tỉ số S 1 / S 2 là:
A. 1 B. 1/2
C. 2/3 D. 3/2
Cho tam giác ABC vuông tại A có BC2a, ACa. Quay tam giác này quanh trục AB, ta được một hình nón đỉnh B. Gọi S1 là diện tích toàn phần của hình nón đó và S2 là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số
S
1
S
2
là:
Đọc tiếp
Cho tam giác ABC vuông tại A có BC=2a, AC=a. Quay tam giác này quanh trục AB, ta được một hình nón đỉnh B. Gọi S1 là diện tích toàn phần của hình nón đó và S2 là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số S 1 S 2 là:
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng ABa,AC
a
3
đường thẳng SÂ tạo với đáy một góc
60
∘
.Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi
S
x
q
l...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng AB=a,AC= a 3 đường thẳng SÂ tạo với đáy một góc 60 ∘ .Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi S x q là diện tích xung quanh của hình nón. Tính S x q
![]()
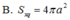
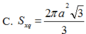
![]()
giúp mình bài này gấp vs ạ
1. tìm họ nguyên hàm của hàm số f(x) = ( 1 + ln x)^2 / x
2. cho hình nón đỉnh S có đáy là hình tròn tâm O. mặt phẳng ( P ) qua S và O cắt hình nón theo thiết diện là một tam giác vuông có diện tích = 2. Tính thể tích khối nón được giới hạn bởi hình nón đã cho
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI R
3
. Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh
S
xq
của hình nón và thể tích V của khối nón là: A.
S
xq
πR
2
;...
Đọc tiếp
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R 3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh S xq của hình nón và thể tích V của khối nón là:
A. S xq = πR 2 ; V = πR 3 3
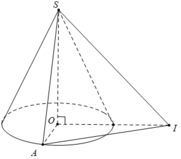
B. S xq = 2 πR 2 ; V = 2 πR 3 3
C. S xq = πR 2 2 2 ; V = πR 3 6
D. S xq = πR 2 ; V = 2 πR 3 3
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng a √2
Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng.
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu
V
1
,
V
2
lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số
V
1
V
2...
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu V 1 , V 2 lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số V 1 V 2 là
![]()
![]()
![]()
![]()
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R3cm, góc ở đỉnh của hình nón là
φ
120
0
. Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
Đọc tiếp
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh của hình nón là φ = 120 0 . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
![]()
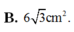
![]()
![]()
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, tính có bán kính của mặt cầu (S)?