Question

Cho tam giác ABC vuông tại A,  BE là tia phân giác của góc B (E thuộc AC) trên BC lấy điểm M sao cho BM = BA

 a) Chứng minh ME⊥ BC

b) Gọi K là giao điểm của ME và AB. Chứng minh EK = EC, BK = BC

c)Chứng minh BE⊥kC

Answer 1

  

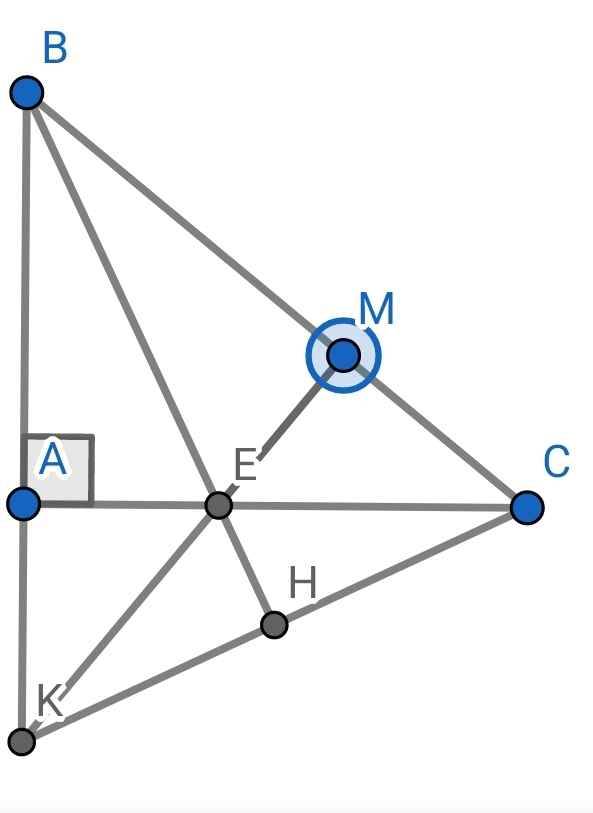
a) Xét ∆ABE và ∆MBE có:

BE chung

góc ABE = góc MBE (BE là phân giác của góc ABC)

AB = BM

⇒∆ABE = ∆MBE (c-g-c)

⇒góc BAE = góc BME (hai góc tương ứng)

⇒ME vuông góc BC

b) Do ∆ABE = ∆MBE (cmt)

⇒AE = ME (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆AEK và ∆MEC có:

AE = ME (cmt)

góc AEK = góc MEC (đối đỉnh)

⇒∆AEK = ∆MEC (cạnh góc vuông - góc nhọn kề)

⇒EK = EC (hai cạnh tương ứng)

AK = MC (hai cạnh tương ứng)

Lại có: BK = BA + AK

BC = BM + MC

⇒BK = BC

c) Gọi H là giao điểm của BE và CK

Xét ∆BHK và ∆BHC có:

BK = BC (cmt)

góc HBK = góc HBC (do BE là tia phân giác của góc ABC)

BH chung

⇒∆BHK = ∆BHC (c-g-c)

⇒góc BHK = góc BHC (hai góc tương ứng)

Mà góc BHK + góc BHC = 180⁰ (kề bù)

⇒góc BHK = góc BHC = 180⁰ : 2 = 90⁰

⇒BH vuông góc KC

Hay BE vuông góc KC