Các câu hỏi tương tự
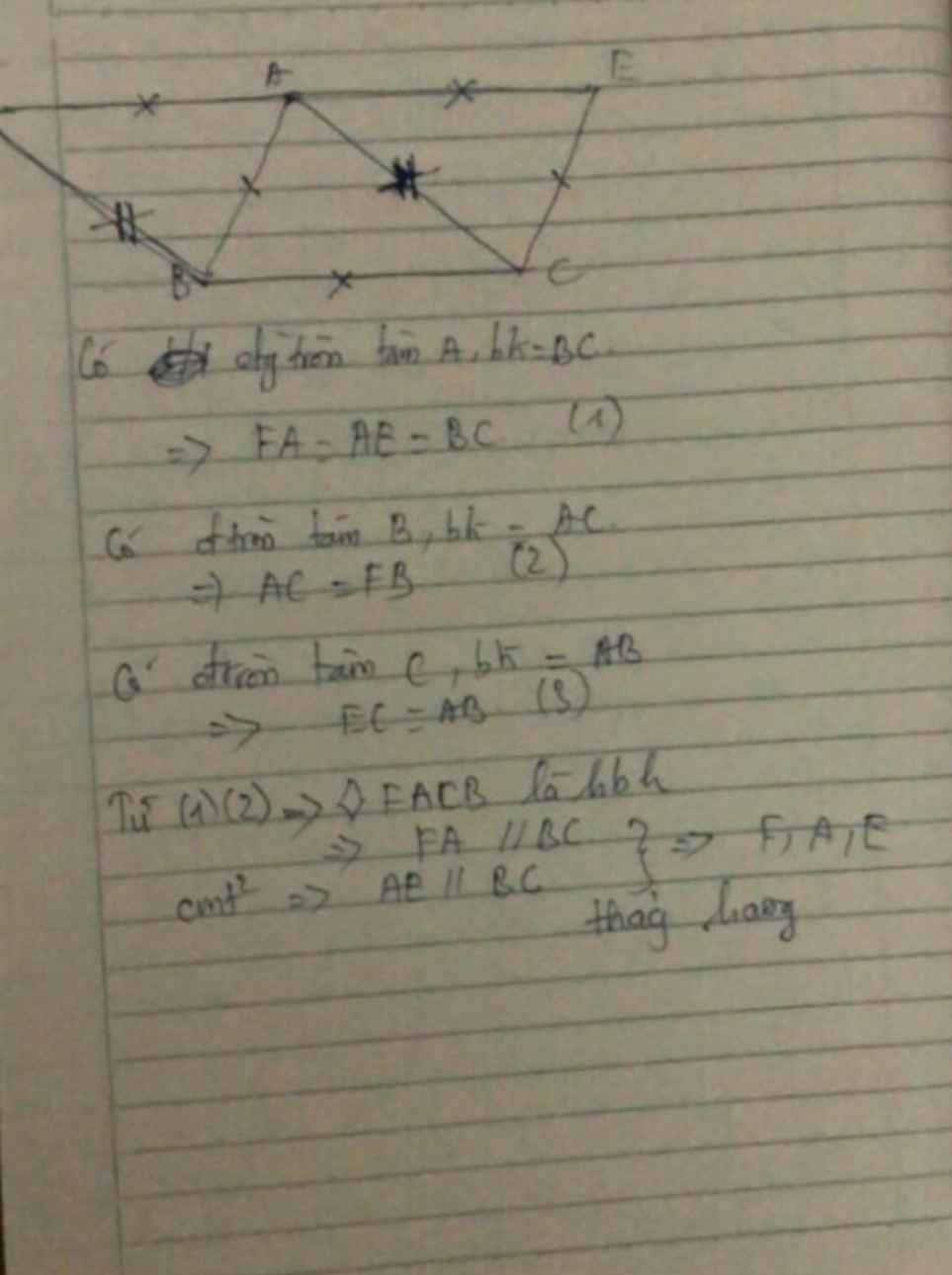
Bài 1:Cho tam giác ABC. Vẽ khung trồn tâm C bán kính AB;Và khung tròn tâm B bán kính AC. Đường tròn tâm A bán kính BC cắt các khung tròn tâm C và B lần lượt tại E và F. ( E,F nằm cùng nửa mặt phẳng bờ BC chứa A. CM 3 điểm F,A,E thẳng hàng
cho tam giác ABC có AB =3cm; BC=4cm. TRên nửa mặt phẳng bờ AC không chứa điểm B, vẽ cung tròn tâm A bán kính 4cm và cung tròn tâm C bán kính 3cm. 2 cung tròn này cắt nhau tại D
a)CMR tam giác ABC=tam giác CAD
b)CMR AB song song CD và AD song song với BC
Cho tam giác ABC. Vẽ đường tròn tâm B bán kính AC, đường tròn tâm C bán kính AB. Hai đường tròn này cắt nhau tại hai điểm E và F thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Chứng minh:
a)ΔABC=ΔECB=ΔFCB
b)AB//CF, AC//BF
c)ΔABE=ΔECA
d)AE//BC
Cho tam giác ABC sao cho AC=AB=3cm. Cho M là trung điểm của BC. Vẽ cung tròn tâm B và cung tròn tâm C đều có bán kính là 3cm và 2 cung tròn cắt nhau tại D,E. Chứng minh A,E,M,D thẳng hàng.
cho tam giác abc nhọn . Trên cùng 1 nửa mặt phẳng bờ AC ko chứa điểm B vẽ cung tròn tâm a bán kính BC , và cung tròn tâm C bán kính AB . gọi D là giao điểm của 2 cung tròn trên . chứng minh rằng :
a) tam giác ABC=tam giác CDA
b) AB//CD
ai bt lm ko giúp mik với
cho tam giác abc có góc c = 30 độ . Trên nửa mặt phẳng ko chứa a bờ bc vẽ cung tròn tam c bán kính ac , vẽ cung tròn tâm b bán kính ba .Hai cung tròn tâm cắt nhau tại d . Tính abd và acd
Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính BA, chúng cắt nhau tại D ( D và B nằm khác phía đối với AC). Chứng minh rằng AD // BC
các bn giúp mình với:
Cho tam giác ABC sao cho AB=AC=3 cm. M là trung điểm của BC. Vẽ cung tròn tâm B(bán kính 3 cm) và cung tròn tâm C(bán kính 3cm) và 2 cung tròn cắt nhau tại D,E. Cho AM là tia phân giác của góc BAC. C/M M,A,D,E thẳng hàng.
Cho tam giác ABC có ba góc nhọn (A > 60o). Về phía ngoài tam giác vẽ các tam giác đều ABD, ACE. Từ D và E vẽ các cung tròn tâm D bán kính AC và tâm E bán kính bằng AB, chúng cắt nhau tại F ( F nằm khác phía với A đối với đường thẳng DE). Chứng minh tam giác FBC là tam giác đều.