Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
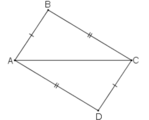
Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)

Cho tam giác ABC. Vẽ cung tròn tâm A bán kính bằng BC, vẽ cung tròn tâm C bán kính bằng BA, chúng cắt nhau ở D ( D và B nằm khác phía đối với AC). Chứng minh AD//BC
Cho tam giác ABC. Vẽ cung tròn tâm A, bán kính BC, vẽ cung tròn tâm C, bán kính BA, chúng cắt nhau tại D(D và B nằm khác phía đối với AC). CMR:AD song song với BC
Cho tam giác ABC . Vẽ cung tròn tâm A bán kính bằng BC , vẽ cung tròn tâm C bán kính bằng BA , chúng cắt nhau ở D ( D và B nằm khác phía đối vs AC ) . C/m rằng AD // BC .
Cho tam giác ABC . Vẽ cung tròn tâm A bán kính bằng BC , vẽ cung tròn tâm C bán kính bằng BA , chúng cắt nhau ở D ( D và B nằm khác phía đối vs AC ) . C/m rằng AD // BC .
Cho tam giác ABC . Vẽ cung tròn tâm A bán kính bằng BC , vẽ cung tròn tâm C bán kính bằng BA , chúng cắt nhau ở D ( D và B nằm khác phía đối vs AC ) . C/m rằng AD // BC .
Cho tam giác ABC, vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính BA, chúng cách nhau ở D (D và B nằm khác phía đối vời bờ AC), CM rằng AD // BC
Cho tam giác ABC.Vẽ cung tròn tâm A bán kinh BC,vẽ cung tròn tâm C bán kính BA, chúng cắt nhau ở D(D và B nắm khác phía đối với bờ AC).Chúng minh rằng AD// BC
Cho tam giác ABC.Vẽ cung tròn tâm A bán kính Bc,vẽ cung tròn tâm B bán kính bằng BA,chúng cắt nhau ở D(D và B nằm khác phía đối với AC).CMR AD//BC
Bài 5. Cho tam giác ABC có 𝐴መ=80. Vẽ cung tròn tâm B bán kính AC, vẽ cung tròn tâm C bán kính BA, hai cung tròn này cắt nhau tại D nằm khác phía của A đối với BC.
a)Tính góc BDC;
b)Chứng minh CD // AB.