a) Ta có: \(AD=\dfrac{1}{2}DC\)(gt)
mà \(EC=ED=\dfrac{DC}{2}\)(E là trung điểm của DC)
nên AD=EC=ED
b) Xét ΔCDB có
M là trung điểm của BC(gt)
E là trung điểm của CD(gt)
Do đó: ME là đường trung bình của ΔCDB(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//BD và \(ME=\dfrac{1}{2}BD\)(Định lí 2 về đường trung bình của tam giác)
hay ME//ID
Xét tứ giác MEDB có ME//BD(cmt)
nên MEDB là hình thang có hai đáy là ME và BD(Định nghĩa hình thang)
c) Xét ΔAME có
D là trung điểm của AE(AD=DE, D nằm giữa A và E)
DI//ME(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
hay IA=IM(Đpcm)
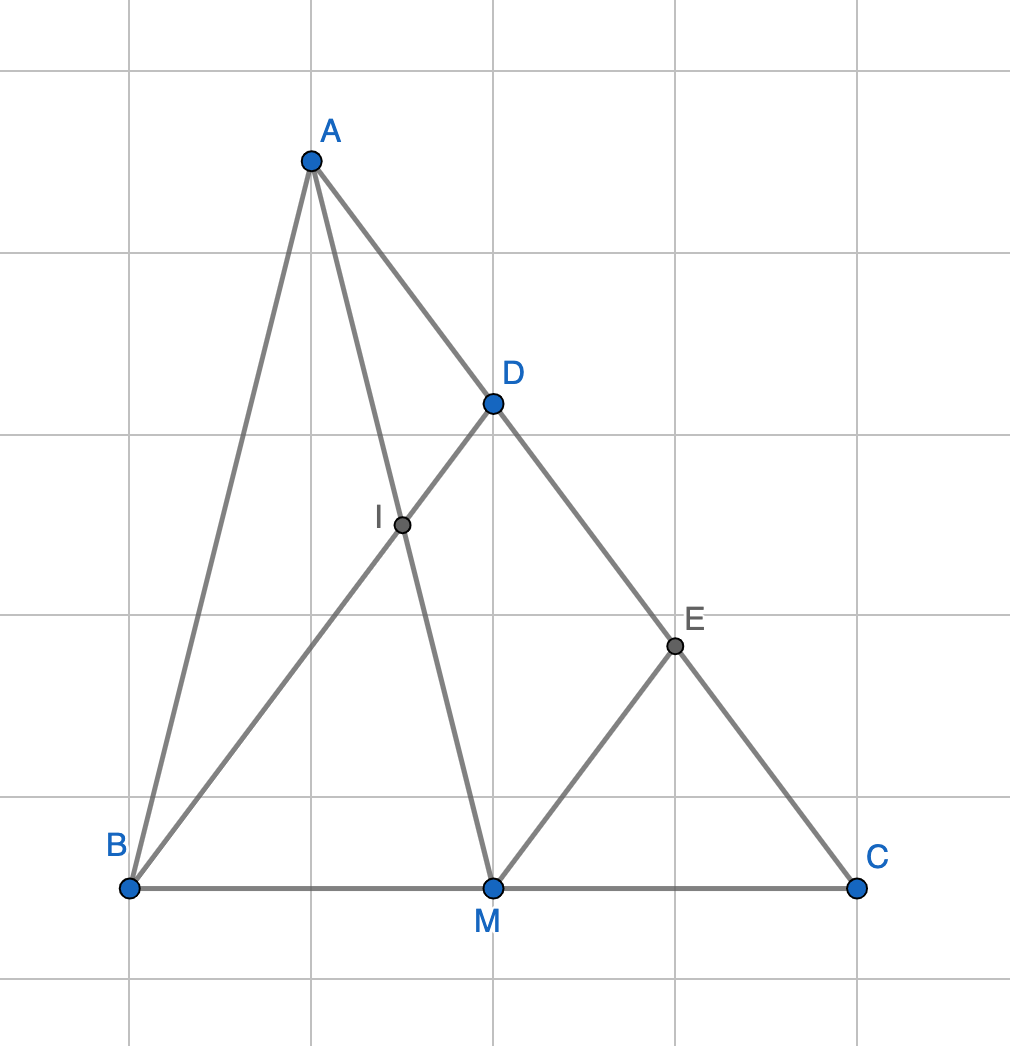
\(a.\) Ta có: DA=\(^{\dfrac{1}{2}DC=DE=EC}\) (đpcm)
\(b.\) Xét tam giác DBC có:
\(\left\{{}\begin{matrix}DE=CE\\BM=CM\end{matrix}\right.\) \(\Rightarrow\) ME là đường trung bình tam giacs DBC
\(\Rightarrow ME\)//\(BD\) \(\Rightarrow\) DEMB là hình thang
\(c.\)Vì \(\Rightarrow ME\)//\(BD\) nên ME // ID
Xét tam giác AMD có: \(\left\{{}\begin{matrix}ME\backslash\backslash ID\\AD=DC\end{matrix}\right.\)
=> ME là đường trung bình tam giác AMD hay I là trung điểm MA
\(\Rightarrow IA=IM\) (đpcm)
a) Ta có: \(DA=\dfrac{DC}{2}\)(gt)
mà \(DE=EC=\dfrac{DC}{2}\)(E là trung điểm của DC)
nên DA=DE=EC
b) Xét ΔDBC có
M là trung điểm của BC(gt)
E là trung điểm của DC(gt)
Do đó: ME là đường trung bình của ΔDBC(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//BD và \(ME=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)
Xét tứ giác DEMB có ME//BD(cmt)
nên DEMB là hình thang có hai đáy là ME và BD(Định nghĩa hình thang)
c) Xét ΔAME có
D là trung điểm của AE
DI//ME(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
Suy ra: IA=IM(Đpcm)
















