a, HS tự chứng minh
b, ∆ADE:∆ACD (g.g)
=> A D 2 = A E . A C
c, Tương tự: ∆ADF:∆ABD => A D 2 = A B . A F => ĐPCM

a, HS tự chứng minh
b, ∆ADE:∆ACD (g.g)
=> A D 2 = A E . A C
c, Tương tự: ∆ADF:∆ABD => A D 2 = A B . A F => ĐPCM
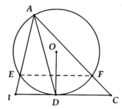
Cho tam giác ABC phân giác AD. Vẽ đường tròn (O) đi qua A, D và tiếp xú với BC tại D. Đường tròn này cắt AB,AC lần lượt tại E và F. Chứng minh:
a) AD\(^2\)=AE.AC b) AE.AC=AB.AF
Cho tam giác ABC phân giác AD. Vẽ đường tròn (O) đi qua A, D và tiếp xúc với BC tại D. Đường tròn này cắt AB, AC lần lượt tại E và F. Chứng minh :
a) EF// BC ( đã làm)
b) AD2 = AE.AC (chưa làm được)
c) AE.AC= AB.AF (đã làm được)
Tôi nhờ các bạn giải hộ câu b. Xin cảm ơn các bạn
Cho tam giác ABC có đường phân giác AD . Vẽ đường tròn (O) đi qua hai điểm A,D và tiếp xúc BC tại D.Đường tròn này cắt BC tại D.Đường tròn này cắt AB,AC tại E,F.Chứng Minh:
a) EF//BC
b) AD\(^2\) =AE.AC
c) AE.AC = AB.AF
Cho tam giác ABC phân giác AD. Vẽ đường tròn (O) đi qua A, D và tiếp xú với BC tại D. Đường tròn này cắt AB,AC lần lượt tại E và F. Chứng minh:
a)
cho tam giác ABC phân giác AD vẽ đg ròn tâm O đi qua A và D tiếp xúc với BC tại D đg tròn cắt AB ,AC tại E và F
a,cm EF//BC
b,AE.AC=\(AD^2\)
c, AE.AC=AB.AF
Cho tam giác ABC có AD là phân giác của góc A . Vẽ đường tròn O đi qua A và D đòng thời tiếp xúc BC tại D . Dường tròn này cắt AB , AC ở E và F.
CMR : a) EF song song AB
b) tam giác AED đòng dạng ADC , tam giác AFD đồng dạng ADB
c) AE.AC=AF.AB=AD^2
cho tam giác ABC,phân giác AD.vẽ đường tròn O qua A và tiếp xúc với C tại D và cắt cạnh AB và AC lần lượt ở E và F.CM EF song song BC
Cho tam giác ABC ngoại tiếp đường tròn (I). Các cạnh AB, BC, CA lần lượt tiếp xúc đường tròn (I) tại các tiếp điểm là D, E, F. Qua A kẻ đường thẳng song song với BC, đường thẳng này cắt tia EF tại K.
a) Chứng minh: AD = AK.
b) Qua D kẻ đường thẳng song song với BC, đường thẳng này cắt đoạn thẳng EF ở M. Các đoạn thẳng AE và DM cắt nhau ở N. Chứng minh NM = ND.
Cho tam giác ABC, phân giác AD. Đường tròn tâm O qua A và tiếp xúc
với BC tại D cắt các cạnh AB và AC lần lượt ở E và F.
a) Chứng minh: EF // BC
b) Chứng minh: AB. BE = BD 2
c) Chứng minh: ADF đồng dạng với ABD
d) Chứng minh: DF là tiếp tuyến của đường tròn đi qua A, B, D.