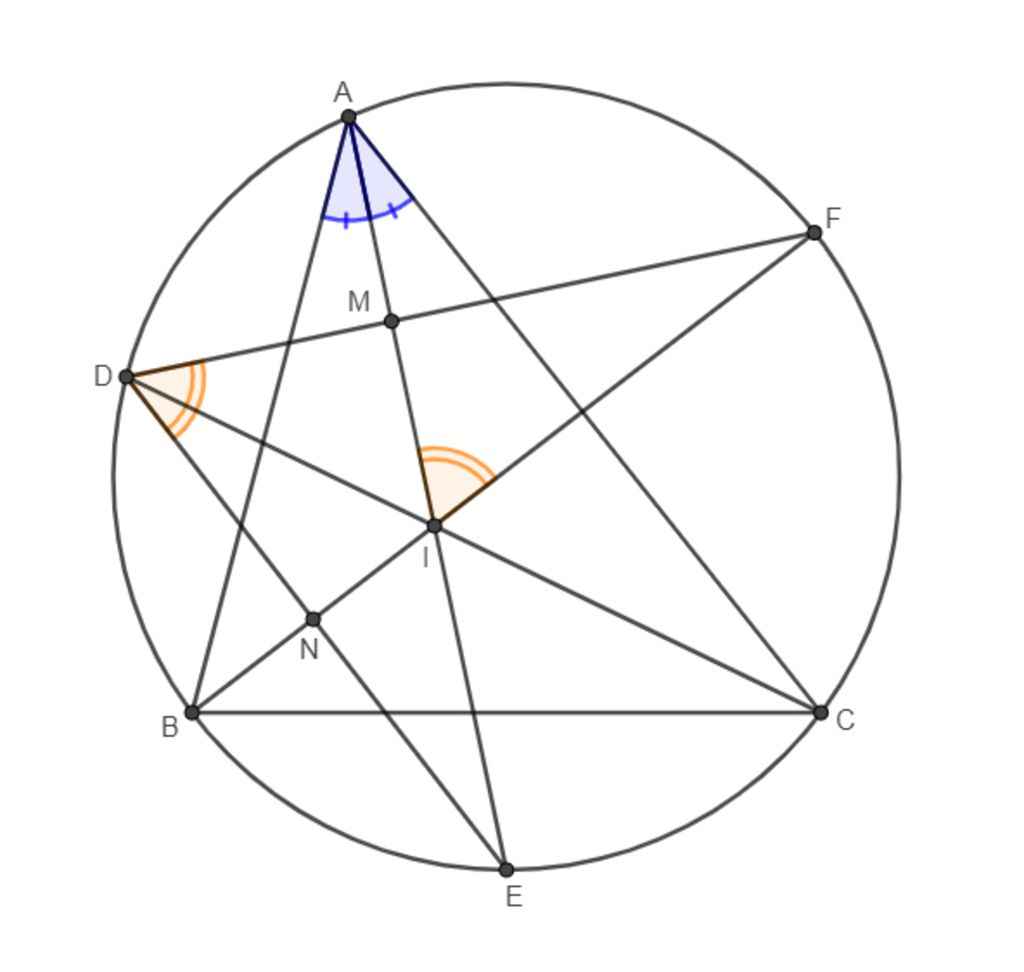
Cho tam giác ABC nội tiếp trong đường tròn: D,E,F theo thứ tự là điểm chính giữa của các cung AB,AC,CA. Gọi I là giao điểm của AE với CD a) Chứng minh AE là đường phân giác của góc BAC. Tìm tâm đường tròn nội tiếp tam giác ABC b) Gọi M là giao điểm của AI với DF, N là giao điểm của BI với DE. CMR DMIN là tứ giác nội tiếp
a) ta có :
\(E\) là điểm chính giữa \(\stackrel\frown{BC}\) \(\left(gt\right)\)
\(\Rightarrow\) \(\stackrel\frown{BE}\) \(=\) \(\stackrel\frown{EC}\)
\(\Rightarrow\widehat{BAE}\) \(=\) \(\widehat{CAE}\) ( góc nội tiếp tương ứng )
\(\Rightarrow\) \(AE\) là phân giác của \(\widehat{BAC}\)
chứng minh tương tự , ta được :
\(CD\) là phân giác của \(\widehat{ACB}\)
ta lại có : \(AE\cap CD=\left\{I\right\}\)
\(\Rightarrow\) \(I\) là tâm đường nội tiếp \(\Delta ABC\)
b) có : \(\widehat{AIF}\) \(=\) \(\dfrac{1}{2}\left(sđ\stackrel\frown{AF}+\stackrel\frown{BE}\right)\)
\(\Leftrightarrow\) \(\widehat{AIF}\) \(=\) \(\dfrac{1}{2}\left(sđ\stackrel\frown{CF}+\stackrel\frown{CE}\right)\)
\(\Leftrightarrow\) \(\widehat{AIF}\) \(=\) \(\dfrac{1}{2}sđ\stackrel\frown{EF}\)
ta lại có :
\(\widehat{EDF}\) \(=\) \(\dfrac{1}{2}sđ\stackrel\frown{EF}\) ( góc nội tiếp chắn \(\stackrel\frown{EF}\) )
do vậy : \(\widehat{AIF}\) \(=\) \(\widehat{EDF}\)
hay : \(\widehat{MIF}\) \(=\) \(\widehat{MDN}\)
xét tứ giác \(DMIN\) có :
\(\widehat{MIF}\) \(=\) \(\widehat{MDN}\)
do đó : \(DMIN\) là tứ giác nội tiếp