TK:
a) Vẽ hình:
``` C
/ \
/ \
E / \ D
/ \
/ \
/___________\
B I A
/
/
O
b) Chứng minh tứ giác BECD nội tiếp được trong đường tròn:
Ta có:
- Tia phân giác trong của góc B cắt tia phân giác trong của góc C tại O (tâm đường tròn nội tiếp tam giác ABC).
- Tia phân giác ngoài của góc B cắt tia phân giác ngoài của góc C tại O (tâm đường tròn ngoại tiếp tam giác ABC).
- Do đó, tứ giác BECD được tạo thành từ các góc B, C, và các tia phân giác trong và ngoài của chúng. Do đó, tứ giác BECD nội tiếp trong đường tròn.
c) Chứng minh BI.IC = ID.IE:
Ta có:
- Theo định lí Ptolemy trong tứ giác nội tiếp, ta có: \( BI \cdot IC + CI \cdot IB = BC \cdot IO \).
- Ta cũng biết rằng \( BC \cdot IO = BM \cdot MC \) (vì \( M \) là điểm trên cung nhỏ \( BC \)).
- Từ hai phương trình trên, ta suy ra: \( BI \cdot IC + CI \cdot IB = BM \cdot MC \).
- Khi đó, ta thấy tứ giác \( BEID \) cũng nội tiếp trong đường tròn, do đó, ta áp dụng lại định lý Ptolemy cho tứ giác \( BEID \), ta có: \( BI \cdot ID + DI \cdot IB = BD \cdot IE \).
- Nhưng \( BD \cdot IE = BM \cdot MC \) (vì \( E, D, M \) thẳng hàng), thay vào biểu thức trước, ta được: \( BI \cdot IC + CI \cdot IB = BI \cdot ID + DI \cdot IB \).
- Loại bỏ \( BI \cdot IB \) ở hai vế, ta được \( BI \cdot IC = ID \cdot IE \).
a: 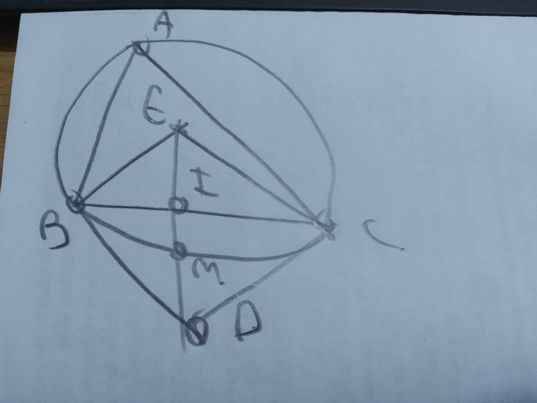
b: Vì BE và BD lần lượt là phân giác của góc trong và góc ngoài tại B
và góc trong và góc ngoài tại đỉnh B là hai góc kề bù
nên BE\(\perp\)BD
Vì CE và CD lần lượt là phân giác của góc trong và góc ngoài tại C
và góc trong và góc ngoài tại đỉnh C là hai góc kề bù
nên CE\(\perp\)CD
Xét tứ giác EBDC có \(\widehat{EBD}+\widehat{ECD}=90^0+90^0=180^0\)
nên EBDC là tứ giác nội tiếp
c: ta có: EBDC là tứ giác nội tiếp
=>\(\widehat{DEC}=\widehat{DBC}\)
Xét ΔIEC và ΔIBD có
\(\widehat{IEC}=\widehat{IBD}\)
\(\widehat{EIC}=\widehat{BID}\)(hai góc đối đỉnh)
Do đó; ΔIEC~ΔIBD
=>\(\dfrac{IE}{IB}=\dfrac{IC}{ID}\)
=>\(IE\cdot ID=IB\cdot IC\)















