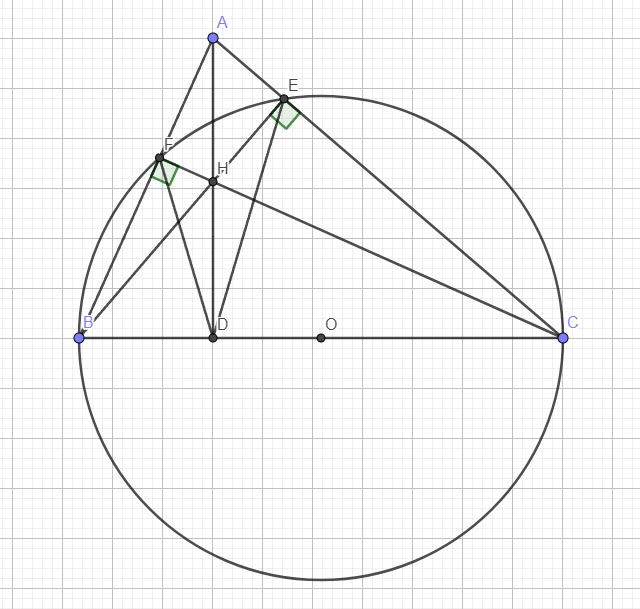
a.
BC là đường kính và E, F thuộc đường tròn (O) nên \(\widehat{BEC}\) và \(\widehat{BFC}\) là các góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BEC}=\widehat{BFC}=90^0\)
\(\Rightarrow\widehat{AEH}=\widehat{ÀH}=90^0\)
\(\Rightarrow E\) và F cùng nhìn AH dưới 1 góc vuông nên AEHF nội tiếp
Do \(\widehat{BEC}=\widehat{BFC}=90^0\Rightarrow\left\{{}\begin{matrix}BE\perp AC\\CF\perp AB\end{matrix}\right.\)
\(\Rightarrow H\) là trực tâm của tam giác ABC
\(\Rightarrow AD\) là đường cao thứ 3 của tam giác ABC
\(\Rightarrow\widehat{ADC}=90^0\)
\(\Rightarrow\) D và F cùng nhìn AC dưới 1 góc vuông nên ADĐC nội tiếp
b.
Câu này em ghi đề sai, đề đúng là: DA là phân giác \(\widehat{EDF}\)
Theo câu a, AFDC nội tiếp \(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF) (1)
Lại có D và E cùng nhìn CH dưới 1 góc vuông \(\Rightarrow CDHE\) nội tiếp
\(\Rightarrow\widehat{HDE}=\widehat{HCE}\) (cùng chắn HE)
Hay \(\widehat{ADE}=\widehat{ACF}\) (2)
(1);(2) \(\Rightarrow\widehat{ADF}=\widehat{ADE}\)
\(\Rightarrow DA\) là phân giác của \(\widehat{EDF}\)