ý của bạn là cotang đk ạ chứ mình thấy cos nó sai ý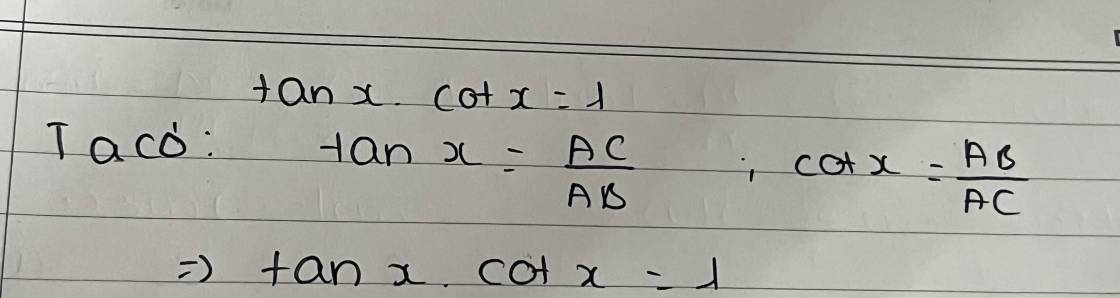
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
CHO TAM GIÁC ABC CÓ AB=6,AC=8,BC=10.ĐƯỜNG CAO AH .GỌI E,F LÀ HÌNH CHIẾU CỦA H LÊN AB VÀ AC
a)CMR: TAM GIÁC ABC VUÔNG
b)TÍNH EF ,đường phân giác AD
c)CMR:AE.AB=AF.AC
d)TÍNH A = SIN2B+SIN2C- TAN B.TAN C
^^ MONG MỌI NGƯỜI GIÚP MÌNH VỚI NHA ^^
Cho tam giác ABC nhọn, các đường cao AK, BD, CE cắt nhau tại H.
1. Chứng minh: \(\dfrac{KC}{KB}=\dfrac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\)
2.Giả sử: \(HK=\dfrac{1}{3}AK.\) Chứng minh rằng: tan B . tan C = 3
Cho tam giác ABC vuông tại A a) chứng minh tanB + cosB lớn hơn bằng 2 b) Khi sinB + cosB=căn 2 . Hãy tính góc B c) H là trung điểm AB, đường thẳng qua H vuông góc với BC tại I và cắt tia AC tại K. Chứng minh tan C x tan BKC =2
GIÚP DÙM MÌNH NHA MÌNH ĐANG CẦN GẤP ^^1/Chứng minh:a) tan^2alpha-sin^2alphacdottan^2alphasin^2alphab)cos^2alpha+tan^2alphacdotcos^2alpha12/Cho tam giác ABC có BH là đường cao, biết AB 40cm;AC58cm;BC42cma) Chứng minh tam giác ABC vuôngb) Tính tỉ số lượng giác của widehat{A}C)Vẽ HEperp AB;HFperp BC. Tính BH ; BE; BF và S_{EFCA}
Đọc tiếp
GIÚP DÙM MÌNH NHA MÌNH ĐANG CẦN GẤP ^^
1/Chứng minh:
a) \(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha=\sin^2\alpha\)
b)\(\cos^2\alpha+\tan^2\alpha\cdot\cos^2\alpha=1\)
2/Cho tam giác ABC có BH là đường cao, biết AB = 40cm;AC=58cm;BC=42cm
a) Chứng minh tam giác ABC vuông
b) Tính tỉ số lượng giác của \(\widehat{A}\)
C)Vẽ \(HE\perp AB;HF\perp BC\). Tính BH ; BE; BF và \(S_{EFCA}\)
1)Cho tam giác ABC vuông tại A.Biết góc B=60 độ;BC=4.Tính AB,AC,chiều cao AH
2)Cho tam giác ABC vuông tại A.Biết AB=2;góc C=45 độ.Tính AC,BC,chiều cao AH
3)Cho tam giác ABC vuông tại A,Biết AB=3;AC=4.Tính sin C,tan B
Giải giúp mình ạ
Thật ra là lớp 10 ạ (Em có khoảng 50 bài và còn vài bài nữa thôi mong mn giúp em mai em phải nộp rồi)
Chứng minh rằng các biểu thức sau không phụ thuộc vào x:
a) \(A=cos^2\left(a+x\right)+cos^2x-2cosacosxcos\left(a+x\right)\)
Cho tam giác ABC. Cm:
a) \(tan\frac{A}{2}tan\frac{B}{2}+tan\frac{B}{2}tan\frac{C}{2}+tan\frac{A}{2}tan\frac{C}{2}=1\)
Cho tam giác ABC nhọn; các đường cao AK; BD; CE cắt nhau tại H.
a ) Chứng minh : \(\frac{KC}{KB}=\frac{AC^2+CB^2-BA^2}{CB^2+BA^2-AC^2}\)
b ) Gỉa sư \(HK=\frac{1}{3}AK\). Chứng minh rằng \(\tan B.\tan C=3\)
c ) giả sử \(S_{ABC}=120cm^2;\widehat{BAC}=60^0\) . . Hãy tính diện tích tam giác ADE?
TAM GIÁC ABC CÓ CÁC GÓC THỎA MÃN:
\(\tan\frac{A}{2}+\tan\frac{B}{2}\)\(\le\tan\frac{A}{2}+\cot\frac{B}{2}\le\)\(2\cot\frac{C}{2}\)
CHỨNG MINH TAM GIÁC ABC LÀ TAM GIÁC ĐỀU
TAM GIÁC ABC CÓ CÁC GÓC THỎA MÃN:
\(\tan\frac{A}{2}+\tan\frac{B}{2}\)\(\le\tan\frac{C}{2}\)VÀ \(\cot\frac{A}{2}+\cot\frac{B}{2}\le2\cot\frac{C}{2}\)
CHỨNG MINH TAM GIÁC ABC LÀ TAM GIÁC ĐỀU











