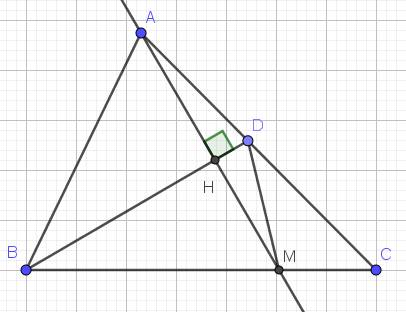
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK
Cho tam giác ABC cân tại A với góc A = 100 độ. Tia phân giác của góc B cắt AC tại D. Qua A kẻ đường thẳng vuông góc với BD và cắt BC tại I.
a.Chứng minh BA=BI
b.Trên tia đối của DB lấy K sao cho DA=DK. Chứng minh tam giác AIK đều
c.Tính các góc của tam giác BCK