Question

Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn tâm O, có AD, BM và CN là ba đường cao cắt nhau tại H. a) Chứng minh tứ giác BNMC và AMHN nội tiếp đường tròn. b) Gọi I và K lần lượt là trung điểm của BC và AH. Chứng minh IK vuông góc với MN và KM là tiếp tuyến của đường tròn đường kính BC.

Answer 1

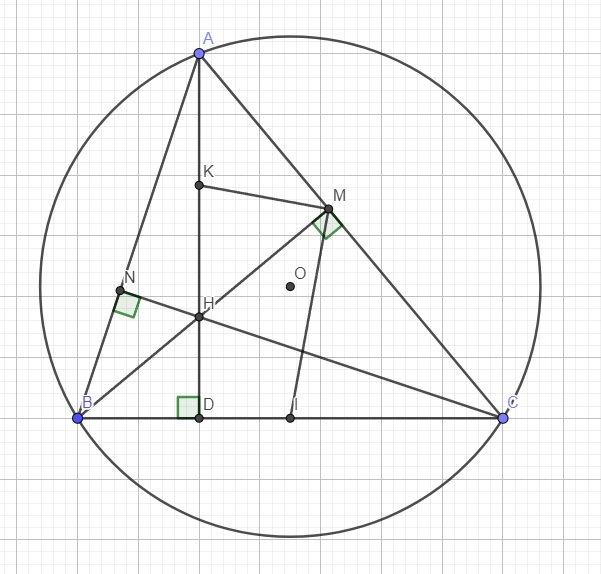
a.

Do CN, BM là các đường cao \(\Rightarrow\widehat{BMC}=\widehat{BNC}=90^0\)

\(\Rightarrow\) M, N cùng nhìn BC dưới 1 góc vuông nên BNMC nội tiếp đường tròn đường kính BC

Cũng do BM, CN là đường cao \(\Rightarrow\widehat{AMH}=\widehat{ANH}=90^0\)

\(\Rightarrow\) M, N cùng nhìn AH dưới 1 góc vuông nên AMHN nội tiếp đường tròn đường kính AH

b.

I là trung điểm BC \(\Rightarrow\) I là tâm đường tròn ngoại tiếp BNMC \(\Rightarrow IM=IN\)

K là trung điểm AH \(\Rightarrow\) K là tâm đường tròn ngoại tiếp AMHN \(\Rightarrow KM=KN\)

\(\Rightarrow IK\) là trung trực MN 

\(\Rightarrow IK\perp MN\)

Do K là tâm đường tròn ngoại tiếp AMHN \(\Rightarrow KM=KH\)

\(\Rightarrow\Delta KMH\) cân tại K

\(\Rightarrow\widehat{KMH}=\widehat{KHM}\)

Tương tự ta có \(\widehat{IMB}=\widehat{IBM}\)

Lại có \(\widehat{KHM}=\widehat{BHD}\) (đối đỉnh)

Mà \(\Delta BHD\) vuông tại D (gt) \(\Rightarrow\widehat{BHD}+\widehat{IBM}=90^0\)

\(\Rightarrow\widehat{KMH}+\widehat{IMB}=90^0\)

\(\Rightarrow\widehat{KMI}=90^0\) hay \(KM\perp IM\)

Mà IM là 1 bán kính của đường tròn đường kính BC

\(\Rightarrow KM\) là tiếp tuyến của đường tròn đường kính BC

Answer 2

Answer 3

a) xét (O) có BM và CN là đường cao => góc BMA và góc CNA = 90^o

xét tg ANHM có:
góc BMA + góc CNA = 90^o + 90^o = 180^o
mà 2 góc này đối nhau => tg ANHM nội tiếp

c/m BNMC nội tiếp thì giống thầy Lâm nhé,câu b mình ko bt làm