Các câu hỏi tương tự
Cho tam giác cân ABC (AB AC; góc A tù). Trên cạnh BC lấy điểm D,trên tia đối của tia CB lấy điểm E sao cho BD CE; Trên tia đối của tia CA lấyđiểm K sao cho CK CA.a) Chứng minh: tam giác ABD tam giác KCEb) Chứng minh: AB + AC AD + AEc) Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB và AItheo thứ tự tại M và N. Gọi O là giao điểm của MN với DE. Chứng minh rằngchu vi tam giác ABC nhỏ hơn chu vi tam giác AMN.d) Chứng minh rằng đường thẳng qua O và vuông góc với MN luôn điqua một điểm...
Đọc tiếp
Cho tam giác cân ABC (AB = AC; góc A tù). Trên cạnh BC lấy điểm D,
trên tia đối của tia CB lấy điểm E sao cho BD = CE; Trên tia đối của tia CA lấy
điểm K sao cho CK = CA.
a) Chứng minh: tam giác ABD = tam giác KCE
b) Chứng minh: AB + AC < AD + AE
c) Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB và AI
theo thứ tự tại M và N. Gọi O là giao điểm của MN với DE. Chứng minh rằng
chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN.
d) Chứng minh rằng đường thẳng qua O và vuông góc với MN luôn đi
qua một điểm cố định khi D di chuyển trên cạnh BC.
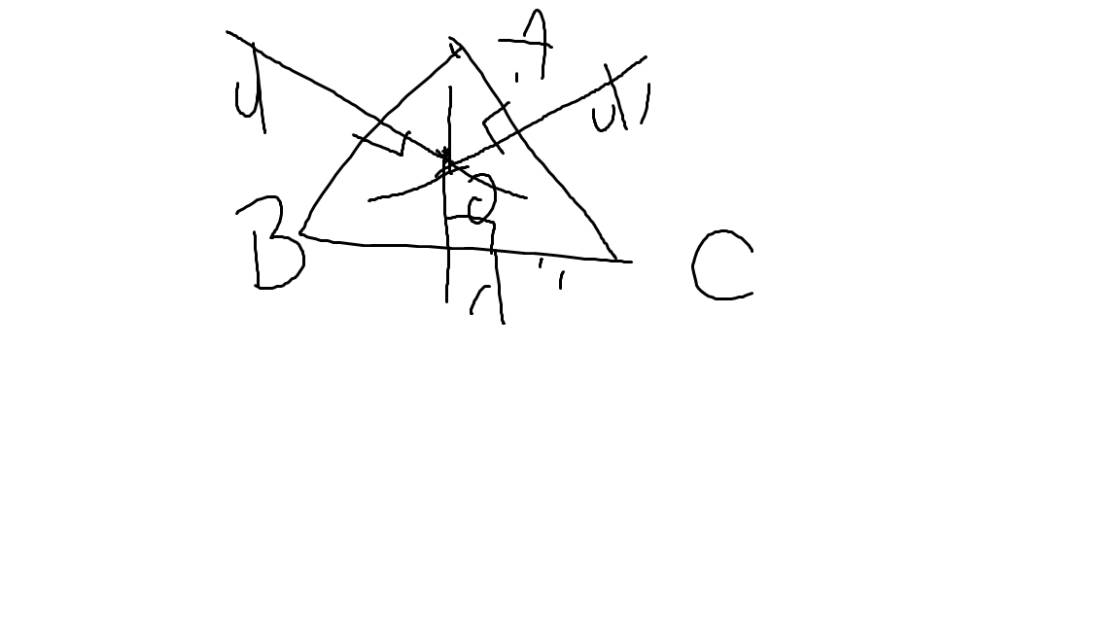
Bài 1: Cho tam giác ABC cân (ABAC), O là giao điểm 3 trung trực 2 cạnh của tam giác ABC (O nằm trong tam giác). Trên tia đối của các tia AB và CA ta lấy 2 điểm M, N sao cho AMCN. Chứng minh:a) Góc OAB góc OCAb) Tam giác AOM tam giác CONc) Hai trung trực OM, ON cắt nhau tại I. Chứng minh OI là tia phân giác của góc MONBài 2: Cho góc nhọn xOy; trên tia Ox lấy 2 điểm A và B (A nằm giữa O, B). Trên Oy lấy 2 điểm C, D (C nằm giữa O, D) sao cho OAOC và OBOD. Chứng minh:a) Tam giác AOD tam giác COBb...
Đọc tiếp
Bài 1: Cho tam giác ABC cân (AB=AC), O là giao điểm 3 trung trực 2 cạnh của tam giác ABC (O nằm trong tam giác). Trên tia đối của các tia AB và CA ta lấy 2 điểm M, N sao cho AM=CN. Chứng minh:
a) Góc OAB = góc OCA
b) Tam giác AOM = tam giác CON
c) Hai trung trực OM, ON cắt nhau tại I. Chứng minh OI là tia phân giác của góc MON
Bài 2: Cho góc nhọn xOy; trên tia Ox lấy 2 điểm A và B (A nằm giữa O, B). Trên Oy lấy 2 điểm C, D (C nằm giữa O, D) sao cho OA=OC và OB=OD. Chứng minh:
a) Tam giác AOD = tam giác COB
b) Tam giác ABD = tam giác CDB
c) Gọi I là giao điểm của AD và BC. Chứng minh IA=IC; IB=ID
Bài 3: Cho tam giác ABC. Qua A kẻ đường thẳng song song với BC, qua C kẻ đường thẳng song song với AB, hai đường thẳng này cắt nhau tại D
a) Chứng minh: AD=BC và AB=DC
b) Gọi M, N lần lượt là trung điểm của BC và AD. Chứng minh: AM=CN
c) Gọi O là giao điểm của AC và BD. Chứng minh: OA=OC và OB=OD
d) Chứng minh: M, O, N thẳng hàng
Bài 4: Cho góc xOy = 60 độ. Vẽ Oz là tia phân giác của góc xOy
a) Tính góc xOy?
b) Trên Ox lấy điểm A và trên Oy lấy điểm B sao cho OA=OB. Tia Oz cắt AB tại I. Chứng minh tam giác OIA = tam giác OIB
c) Chứng minh OI vuông góc AB
d) Trên tia Oz lấy điểm M. Chứng minh MA=MB
e) Qua M vẽ đường thẳng song song với AB cắt tia Ox, Oy lần lượt tại C và D. Chứng minh BD=AC
Mọi ng giúp mình giải bài này nhé! Cảm ơn mn <3
cho tam giác ABC cân đáy Bc,trên đường vuông góc với AC kẻ từ C lấy D sao cho B và D nằm khác phía đối với AC. gọi K là giao điểm của đường thẳng đi qua B vuông góc với AB và đường thẳng đi qua trung điểm M của CD và vuông góc với AD. so sánh KB với KD
Cho tam giác ABC cân ở A. Trên cạnh BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BD CE. Qua D kẻ đường thẳng vuông góc với BC cắt AB ở M. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại N (biết M và N nằm trên hai nửa mặt phẳng đối nhau). Gọi giao điểm của MN với BC là I. Đường vuông góc với MN kẻ qua I cắt tia phân giác của góc BAC ở O. CMR:a) Tam giác MBD tam giác NCE.b) ME // DN.c) Tam giác MON cân tại O.d) OC _|_ AN.
Đọc tiếp
Cho tam giác ABC cân ở A. Trên cạnh BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BD = CE. Qua D kẻ đường thẳng vuông góc với BC cắt AB ở M. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại N (biết M và N nằm trên hai nửa mặt phẳng đối nhau). Gọi giao điểm của MN với BC là I. Đường vuông góc với MN kẻ qua I cắt tia phân giác của góc BAC ở O. CMR:
a) Tam giác MBD = tam giác NCE.
b) ME // DN.
c) Tam giác MON cân tại O.
d) OC _|_ AN.
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AMIK b) Tam giác AMI bằng tam giác IKC c) AIIC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho IDIA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân gi...
Đọc tiếp
Bài 1: Cho tam giac ABC, M là trung điểm cua AB. Đường thẳng qua M và song song với BC cắt AC ở I và song song với AB cắt BC ở k. Chứng minh rằng: a) AM=IK b) Tam giác AMI bằng tam giác IKC c) AI=IC Bài 2: Cho tam giác ABC vuông tại A. Gọi I là trung điểm BC. Trên tia đối của tia IA lấy điểm D sao cho ID=IA a) CMR tam giác BID bằng tam giác CIA b) CMR : BD vuông góc với AB c) Qua A kẻ đường thẳng song song với BC cắt đường thẳng BD tại M. C/M tam giác BAM bằng tam giác ABC d) CMR: AB là tia phân giác cuả góc DAM Bài 3: Cho tam giác ABC vuông ở A và AB=AC.Gọi K là trung điểm của BC a) C/M: tam giác AKB bằng tam giác AKC b) C/M: AK vuông góc với BC c) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E.C/M EK song song với AK Bài 4: Cho tam giác ABC có AB=AC, kẻ BD vuông góc với AC, CE vuông góc với AB(D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. CMR a) BD= CE b) tam giác OEB bằng tam giác ODC c) AO là tia phân giác cua góc BAC
Cho tam giác ABC vẽ một đường thẳng qua A và vuông góc BC tại M trên cạnh AC lấy điểm D Vẽ đường thẳng qua D và vuông góc BC tại N
a, Viết tên các tâm giác có trong hình vẽ
b, Chứng minh MAC=NDC
Cho tan giác ABC và D là điểm nằm giữa hai điểm B,C. Vẽ đường thẳng đi qua D song song với cạnh AB, cắt AC ở E. Vẽ đường thẳng đi qua D song song cạnh AC, cắt AB ở G
a. Tìm các góc ở đỉnh D bằng các góc ở tam giác ABC
b. tính tổng số đo các góc của tam giác ABC
Cho tam giác ABC vẽ một đường thẳng qua A và vuông góc BC tại M trên cạnh AC lấy điểm D Vẽ đường thẳng qua D và vuông góc BC tại N
a, Viết tên các tâm giác có trong hình vẽ
b, Chứng minh MAC=NDC
Cho tam giác ABC cân tại A. Trên BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Qua D và E kẻ các đường thẳng vuông góc với BC cắt AB,AC lần lượt ở M và N. Gọi giao điểm của MN và BC là I. Qua I kẻ đường thẳng vuông góc với MN cắt tia phân giác của BAC tại O. Chứng minh :
a. DM = EN
b. Tam giác OMN cân
c. OC vuông góc với AN .
Xem chi tiết
1)Tam giác ABC có AB30cm, AC40cm. Trên tia đối của tia AC lấy điểm D sao cho ADAB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC.2) Tam giác ABC có ABAC. Gọi d là đường trung trực của BC, E là giao điểm của d với AC. Gọi K là một điểm bất kì thuộc d (K khác E). So sánh chu vi các tam giác AKB và AEB.3) Cho điểm A nằm trong góc nhọn xOy. Vẽ điểm D đối xứng với A qua Ox. Vẽ điểm E đối xứng với A qua Oy. Gọi B và C theo thứ tự là gi...
Đọc tiếp
1)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC.
2) Tam giác ABC có AB<AC. Gọi d là đường trung trực của BC, E là giao điểm của d với AC. Gọi K là một điểm bất kì thuộc d (K khác E). So sánh chu vi các tam giác AKB và AEB.
3) Cho điểm A nằm trong góc nhọn xOy. Vẽ điểm D đối xứng với A qua Ox. Vẽ điểm E đối xứng với A qua Oy. Gọi B và C theo thứ tự là giao điểm của DE với Ox và Oy. Chứng minh rằng tam giác ABC có chu vi nhỏ nhất trong các tam giác có một đỉnh là A, hai đỉnh kia nằm trên các tia Ox và Oy.