Question

cho tam giác ABC đều, kẻ AH vuông góc BC tại H, kẻ HD vuông góc AB tại D, HE vuông góc AC tại E

a) Chứng minh tam giác AHB = tam giác AHC

b) Tam giác ADE là tam giác gì?Vì sao?

c) So sánh DH và HC

HELP ME PLS:>

Answer 1

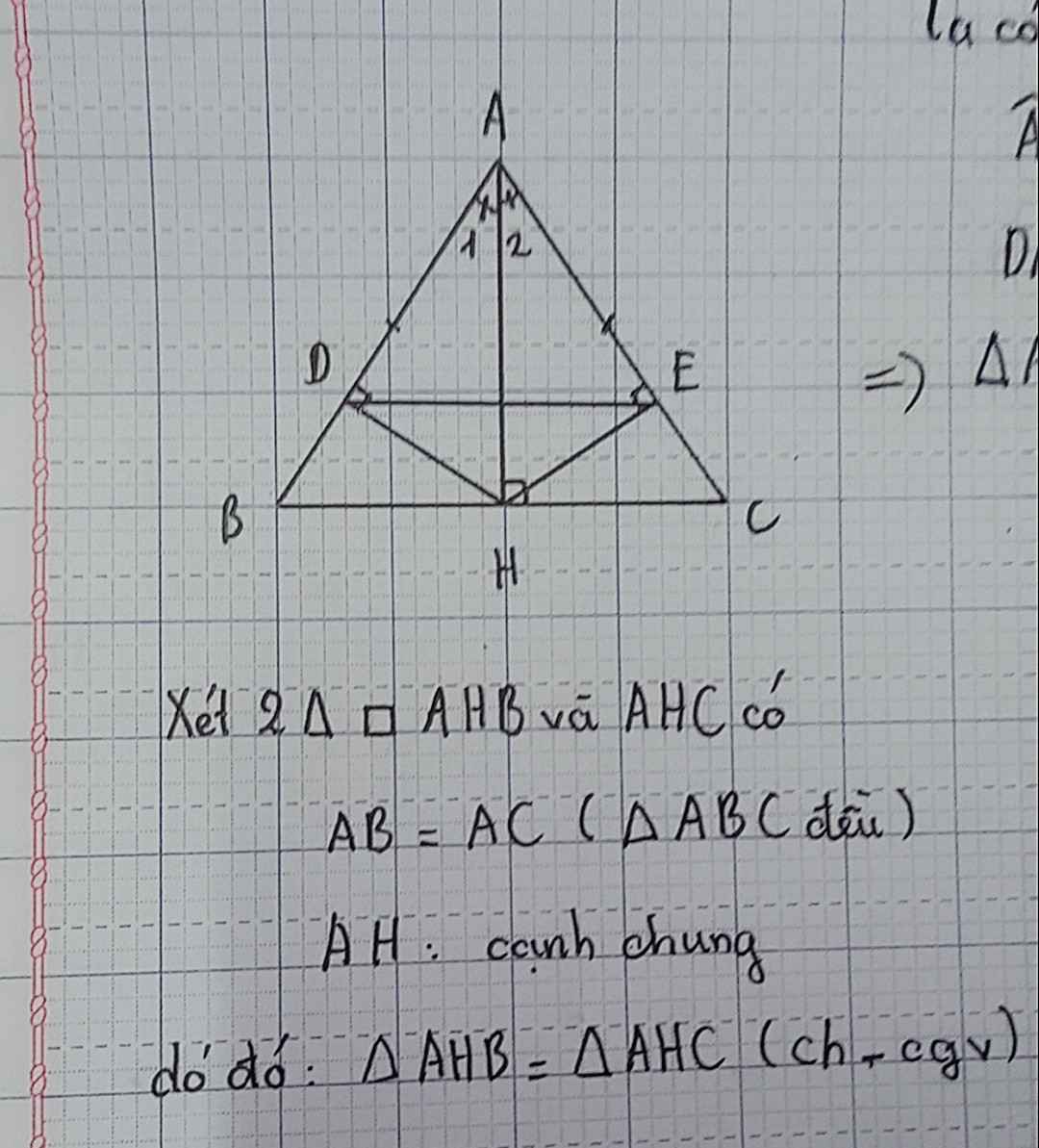
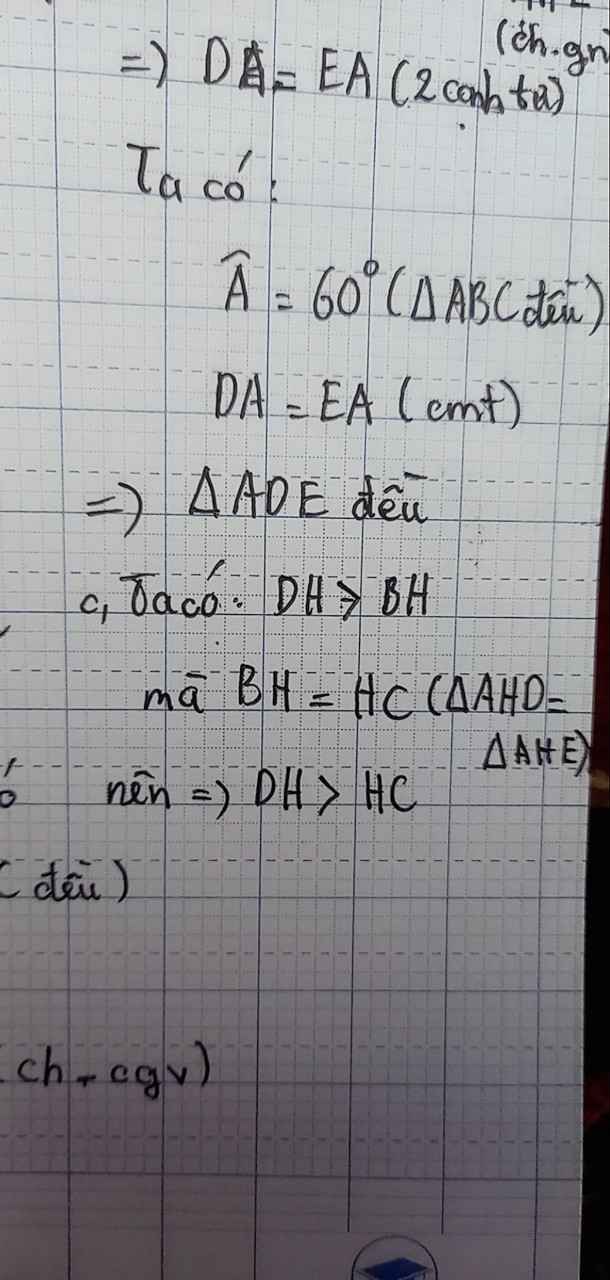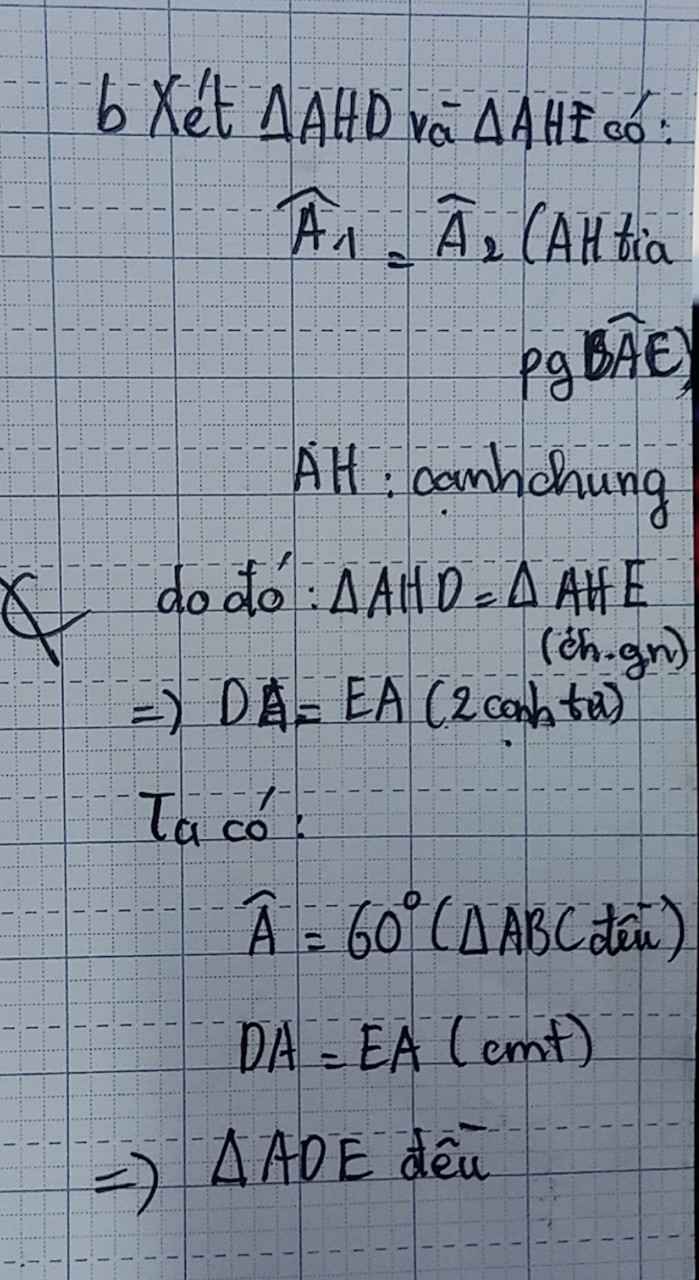a, Xét tg ABH và tg ACH, có:

AB=AC(tg ABC đều)

góc AHB= góc AHC(=90^o)

AH chung

=>tg AHB= tg AHC(ch-cgv)

b, Xét tg ADH và tg AEH, có: 

góc DAH= góc HAE(2 góc tương ứng)

AH chung

góc ADH= góc AEH(=90^o)

=>tg ADH= tg AEH(ch-gn)

=>AD=AE(2 cạnh tương ứng)

=>tg ADE là tg cân tại A.(1)

Mà ta có:tg ABC là tam giác đều nên góc A= góc B= góc C=60^o(2)

Từ (1) và (2), suy ra:

tg ADE là tg đều.

c,Xét tg DBH vuông tại D và tg ECH vuông tại E, có:

BC=CH(2 cạnh tương ứng)(1)

Mà BH>DH(trong tg, cạnh huyền là cạnh lớn nhất)(2)

Từ (1) và (2), suy ra:

DH<CH(đpcm)

 

 

Answer 2