Các câu hỏi tương tự
Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB 2MC. Hãy phân tích vectơ
A
M
→
theo hai vectơ
u
→
A
B
→
;
v
→
A
C
→
Đọc tiếp
Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ A M → theo hai vectơ u → = A B → ; v → = A C →
![]()
![]()
![]()
![]()
Cho tam giác đều ABC . Gọi M,N ,P lần lượt là các điểm thoả mãn vectơ BM = k vectơ BC , 4 vectơ AN = 3 vectơ AB , 3 vectơ AP = 2 vectơ AC . a, Biểu diễn vectơ AM theo hai vectơ AB , AC . b, Tìm k để hai đường thẳng AM , NP vuông góc với nhau.
Cho tam giác ABC gọi M,N,P lần lượt là trung điểm của các cạnh AB,AC,BC a) Tìm các vectơ cùng phương AM b) Tìm các vectơ cùng hướng MN c) Tìm các vectơ ngược hướng BC
Cho tam giác ABC, trên cạnh BC lấy điểm D sao cho BD= 2/3 BC, M là trung điểm của đoạn thẳng AD, điểm N thoả mãn điều kiện vectơ AN = 2/5 vectơ AC. Chứng minh 3 điểm B , M ,N thẳng hàng.
Cho tam giác ABC . Gọi D là điểm sao cho
B
D
→
2
3
B
C
→
và I là trung điểm của cạnh AD , M là điểm thỏa mãn
A
M
→
2
5
A
C
→
Vectơ...
Đọc tiếp
Cho tam giác ABC . Gọi D là điểm sao cho B D → = 2 3 B C → và I là trung điểm của cạnh AD , M là điểm thỏa mãn A M → = 2 5 A C → Vectơ B I → được phân tích theo hai vectơ B A → v à B C → .Hãy chọn khẳng định đúng trong các khẳng định sau?
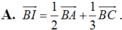
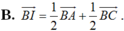
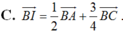
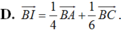
Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ M N → có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P bằng:
A. 1
B. 2
C. 3
D. 6
Cho hình vuông ABCD, gọi MN là trung điểm AD, CD.
a) phân tích vectơ BM, vectơ AN qua 2 vectơ AB và AD
b) Chứng minh: BM vuông góc AN
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho
M
B
→
1
3
M
C
→
. Khi đó vectơ
A
M
→
biểu diễn theo các vectơ
u
→
A
B
→
;
v...
Đọc tiếp
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho M B → = 1 3 M C → . Khi đó vectơ A M → biểu diễn theo các vectơ u → = A B → ; v → = A C → là
A. A M → = 3 2 u → - 1 2 v →
B. A M → = 3 2 v → + 1 2 u →
C. A M → = - 3 2 v → - 1 2 u →
D. A M → = - 3 2 v → + 1 2 u →
Cho ∆ABC, G là trọng tâm. Gọi M,N,P lần lượt là trung điểm của BC,AC,AB. Chứng minh a/ Vectơ BM +NC= PC b/ Vectơ GB +GC+2MG =0







