Các câu hỏi tương tự
Cho tam giác ABC có các cạnh BC=a, AC=b, BC=a và diện tích S=1/4(a+b-c)(a+c-b). Tam giác ABC có dạng đặc biệt nào
A. Tam giác vuông tại B
B. Tam giác đều
C. Tam giác vuông tại C.
D. Tam giác vuông tại A.
Cho tam giác ABC vuông tại A, có
A
B
a
,
B
C
a
10
. Thể tích khối nón khi quay tam giác ABC quanh trục AC là: A.
3
πa
3
B.
9
πa
3
C.
πa
3
D.
10
πa
3
Đọc tiếp
Cho tam giác ABC vuông tại A, có A B = a , B C = a 10 . Thể tích khối nón khi quay tam giác ABC quanh trục AC là:
A. 3 πa 3
B. 9 πa 3
C. πa 3
D. 10 πa 3
Cho tam giác ABC vuông tại A có AB5,
A
B
C
30
°
. Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là A.
100
π
3
B.
200
π
3
C.
50
π
3
D. Kết quả khác
Đọc tiếp
Cho tam giác ABC vuông tại A có AB=5, A B C = 30 ° . Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là
A. 100 π 3
B. 200 π 3
C. 50 π 3
D. Kết quả khác
Cho tam giác ABC là tam giác đều cạnh a, gọi H là trung điểm cạnh BC. Hình nón nhận được khi quay tam giác ABC xung quanh trục AH có diện tích đáy bằng: A.
π
a
2
B.
π
a
2
2
C.
π
a
2
4
D.
π
a...
Đọc tiếp
Cho tam giác ABC là tam giác đều cạnh a, gọi H là trung điểm cạnh BC. Hình nón nhận được khi quay tam giác ABC xung quanh trục AH có diện tích đáy bằng:
A. π a 2
B. π a 2 2
C. π a 2 4
D. π a 2
Trong không gian cho tam giác ABC vuông tại A có
A
B
a
và
B
C
2
a
. Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng A.
πa
3
B.
3
πa
3
C.
3
3
πa
3
D.
2
3
πa...
Đọc tiếp
Trong không gian cho tam giác ABC vuông tại A có A B = a và B C = 2 a . Quay tam giác ABC xung quanh cạnh AB ta thu được khối nón có thể tích bằng
A. πa 3
B. 3 πa 3
C. 3 3 πa 3
D. 2 3 πa 3
Cho tam giác ABC vuông tại A, ABa, BC2a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh trục BC. A.
π
a
3
2
B.
π
a
3
3
C.
3
π
a
3
D.
π
a
3
Đọc tiếp
Cho tam giác ABC vuông tại A, AB=a, BC=2a. Tính thể tích khối nón nhận được khi quay tam giác ABC quanh trục BC.
A. π a 3 2
B. π a 3 3
C. 3 π a 3
D. π a 3
Cho tam giác ABC vuông tại
A
,
AB
6
,
AC
8
.
Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là A.
96
3
π
B.
96
π
C.
384
5
π
D.
1152
5
π
Đọc tiếp
Cho tam giác ABC vuông tại A , AB = 6 , AC = 8 . Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. 96 3 π
B. 96 π
C. 384 5 π
D. 1152 5 π
Cho tam giác ABC vuông tại A,
A
B
6
,
A
C
8
. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là A.
96
3
π
B.
96
π
C.
384
5
π
D.
1152
5
π
Đọc tiếp
Cho tam giác ABC vuông tại A, A B = 6 , A C = 8 . Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. 96 3 π
B. 96 π
C. 384 5 π
D. 1152 5 π
Cho tam giác ABC có hai đỉnh B, C cố định BC 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là A. Đường thẳng x+2y+4a0 D. Parabôn y2ax2
Đọc tiếp
Cho tam giác ABC có hai đỉnh B, C cố định BC = 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là
A. Đường thẳng x+2y+4a=0
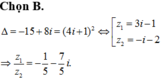
![]()
D. Parabôn y=2ax2


