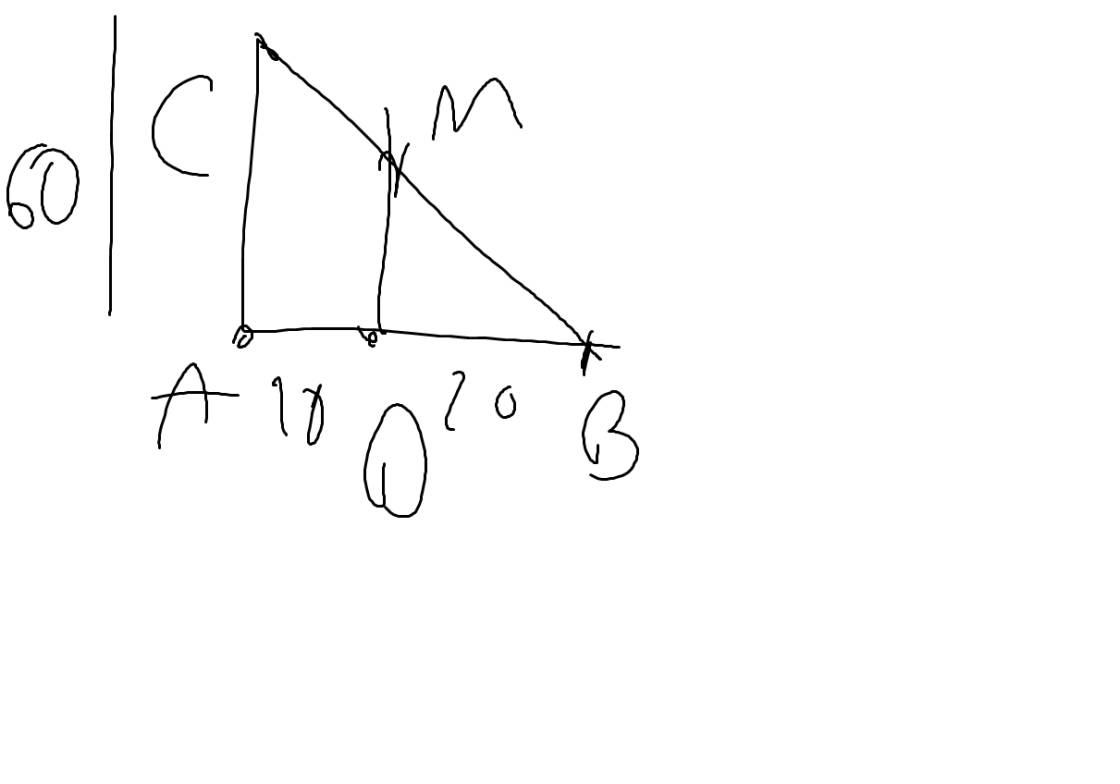Question

Cho tam giác ABC có góc A vuông, cạnh AB = 30cm, cạnh AC = 60cm, MDAC là hình thang có chiều cao 10cm. ( M trên cạnh BC, D trên cạnh AB). Tình diện tích tam giác BMD?

Answer 1

MDAC là hình thang có chiều cao 10cm

=>MD//AC và AD=10cm

DB+AD=AB

=>DB+10=30

=>DB=20(cm)

Xét ΔBAC có MD//AC

nên \(\dfrac{MD}{AC}=\dfrac{BD}{BA}\)

=>\(\dfrac{MD}{60}=\dfrac{20}{30}=\dfrac{2}{3}\)

=>\(MD=60\cdot\dfrac{2}{3}=40\left(cm\right)\)

Diện tích hình thang ADMC là:

\(S_{ADMC}=\dfrac{1}{2}\cdot AD\cdot\left(MD+AC\right)\)

\(=\dfrac{1}{2}\cdot10\cdot\left(60+40\right)=5\cdot100=500\left(cm^2\right)\)

Diện tích tam giác ABC là:

\(S_{ACB}=\dfrac{1}{2}\cdot AB\cdot AC=900\left(cm^2\right)\)

\(S_{ABC}=S_{BMD}+S_{CMDA}\)

=>\(S_{BMD}+500=900\)

=>\(S_{DMB}=400\left(cm^2\right)\)