Các câu hỏi tương tự
Cho tam giác ABC cân tại A . Trên tia đối của tia BC lấy điểm M , trên tia đối của tia CB lấy điểm N sao cho BMCN
a/ chứng minh tam giác AMN cân
b/ kẻ BE vuông góc vs AM , CF vuông góc với AN . Chứng minh tam giác BMEtam giác CMF
c/ EB và FC kéo dài cắt nhau tại O . Chứng minh AO là tia phân giác của góc MAN
d/ qua M kẻ đường thẳng vuông góc với AM , qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H . Chứng minh ba điểm A,O,H thẳng hàng
Đọc tiếp
Cho tam giác ABC cân tại A . Trên tia đối của tia BC lấy điểm M , trên tia đối của tia CB lấy điểm N sao cho BM=CN
a/ chứng minh tam giác AMN cân
b/ kẻ BE vuông góc vs AM , CF vuông góc với AN . Chứng minh tam giác BME=tam giác CMF
c/ EB và FC kéo dài cắt nhau tại O . Chứng minh AO là tia phân giác của góc MAN
d/ qua M kẻ đường thẳng vuông góc với AM , qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H . Chứng minh ba điểm A,O,H thẳng hàng
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác BED bằng tam giác BAD .
b) Tam BCF cân tại B .
c) BD là đường trung tuyến của tam giác BCF .
Đọc tiếp
Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác BED bằng tam giác BAD .
b) Tam BCF cân tại B .
c) BD là đường trung tuyến của tam giác BCF .
Cho tam giác ABC có AB AC BC m m 0 . Trên cạnh Bc lấy D sao cho BD 1 3 BC. Từ D kẻ DE vuông góc BC tại D E thuộc AB , kẻ DF vuông góc AC tại F .a Chứng minh tam giác DEF đềub Lấy điểm M bất kì trên cạnh BC , từ M kẻ MH vuông góc AB tại H, MK vuông góc AC tại K .Tính MH MK 2
Cho tam giác nhọn ABC (BC AC AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI BI. Vẽ các điểm H, K lần lượt là hình chiếu của I trên AB và ADCho tam giác nhọn ABC (BC AC AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI BI. Vẽ các điểm H,K lần lợt là hình chiếu của I trên AB và AD.a) Chứng minh tam giác ABC là tam giác cân.b) Chứng minh IH IK.c) So sánh IH và ID.Giúp mình với ạ
Đọc tiếp
Cho tam giác nhọn ABC (BC > AC > AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI = BI. Vẽ các điểm H, K lần lượt là hình chiếu của I trên AB và AD
Cho tam giác nhọn ABC (BC > AC > AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI = BI. Vẽ các điểm H,K lần lợt là hình chiếu của I trên AB và AD.
a) Chứng minh tam giác ABC là tam giác cân.
b) Chứng minh IH = IK.
c) So sánh IH và ID.
Giúp mình với ạ
Bài 1. Cho tam giác ABC cân tại A, đường trung tuyến AM; AB = 13 cm, BC = 10 cm.
a) Tính độ dài AM.
b) Trên AM lấy điểm G sao cho GM = \(\dfrac{1}{3}\) AM. Tia BG cắt AC tại N. C/m: NA = NC.
c) Tính độ dài BN.
d) Tia CG cắt AB tại L. Chứng minh rằng LN // BC.
cho tam giác ABC vuông tại A Tia phân giác ở góc B cắt AC tại E trên cạnh BC lấy điểm D sao choBD = BA. CMR
a, CMR: tg ABE= tg DBE
b, CMR: ED vuông góc với BC
c, tia DE cắt BA tại K, CMR BK = BC
d, TỪ A kẻ AH vuông góc với BC ''H thuộc BC", AH cắt BE tại I CMR AD là đường trung trực của IE
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. KẺ IH vuông óc với BC (H thuộc BC) . biết HI= 1cm , HB = 2cm,HC=3cm
Tính chu vi tam giác ABC
Giúp liền là đc tiền nè
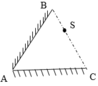
Hai gương phẳng giống nhau AB và AC được đặt hợp với nhau một góc 600, mặt phản xạ hướng vào nhau (A,B,C tạo thành tam giác đều). Một nguồn sáng điểm S di chuyển trên cạnh BC. Ta chỉ xét trong mặt phẳng hình vẽ. a) Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S, phản xạ lần lượt trên AB, AC rồi về S. b) Hãy tính góc tạo bởi tia tới từ S đến gương AB và tia phản xạ cuối cùng. c) Với vị trí nào của S trên BC thì tổng đường đi của tia sáng trong câu a) là bé nhất?
Đọc tiếp
Hai gương phẳng giống nhau AB và AC được đặt hợp với nhau một góc 600, mặt phản xạ hướng vào nhau (A,B,C tạo thành tam giác đều). Một nguồn sáng điểm S di chuyển trên cạnh BC. Ta chỉ xét trong mặt phẳng hình vẽ.
a) Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S, phản xạ lần lượt trên AB, AC rồi về S.
b) Hãy tính góc tạo bởi tia tới từ S đến gương AB và tia phản xạ cuối cùng.
c) Với vị trí nào của S trên BC thì tổng đường đi của tia sáng trong câu a) là bé nhất?
Hai gương phẳng quay mặt phản xạ vào nhau và hợp với nhau 1 góc α. Tiết diện vuông góc với cạnh chung là 1 tam giác cân AOB (cân tại O). Điểm sáng S được đặt ở trung điểm của AB. Xác định α để mọi tia sáng từ S chỉ phản xạ một lần và ra khỏi tam giác AOB của hệ gương

Cho hai gương phẳng hợp với nhau một góc 20 độ và quay mặt phẳn xạ vào nhau. Trên mặt phẳng vuông góc với giao tuyến chung của hai gương ta chiếu 1 tia sáng song song với phân giác của góc hợp bởi hai gương.a) Vẽ tiếp đường đi của tia sáng trênb) Tia sáng trên phản xạ mấy lần trên hai gươngc) Tính góc hợp tia sáng ta chiếu ban đầu và tia phản xạ sau cùng
Đọc tiếp
Cho hai gương phẳng hợp với nhau một góc 20 độ và quay mặt phẳn xạ vào nhau. Trên mặt phẳng vuông góc với giao tuyến chung của hai gương ta chiếu 1 tia sáng song song với phân giác của góc hợp bởi hai gương.
a) Vẽ tiếp đường đi của tia sáng trên
b) Tia sáng trên phản xạ mấy lần trên hai gương
c) Tính góc hợp tia sáng ta chiếu ban đầu và tia phản xạ sau cùng












