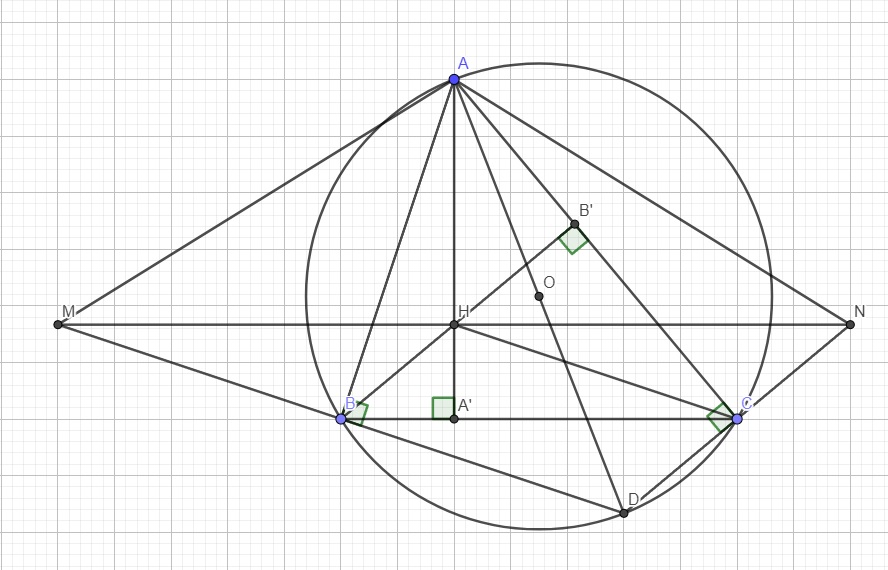
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O,các đường cao AA' và BB' cắt nhau tại H.AO cắt đường tròn tại D.
a) CM: tứ giác ABA'B' nội tiếp được đường tròn.
b) CM: tứ giác BHCD là hình bình hành.
c) Gọi điểm M đối xứng với D qua AB,N đối xứng với D qua AC.CM: 3 điểm M,H,N thẳng hàng.
(GIÚP MÌNH CẢ CÂU C NHA!)
a.
Do AA', BB' là các đường cao \(\Rightarrow\widehat{AA'B}=\widehat{AB'B}=90^0\)
\(\Rightarrow A';B'\) cùng nhìn AB dưới 1 góc vuông nên ABA'B' nội tiếp
b.
Do AD là đường kính \(\Rightarrow\widehat{ACD}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACD}=90^0\Rightarrow DC\perp AC\)
Mà \(BH\perp AC\) (gt)
\(\Rightarrow BH||DC\)
Chứng minh tương tự ta có \(CH||DB\)
\(\Rightarrow BHCD\) là hình bình hành (2 cặp cạnh đối song song)
c.
N đối xứng D qua AC \(\Rightarrow DN\perp AC\)
Mà \(DC\perp AC\) (cmt) \(\Rightarrow D,C,N\) thẳng hàng hay C là giao điểm của DN và AC
\(\Rightarrow DC=CN\)
Theo câu b, BHCD là hbh \(\Rightarrow\left\{{}\begin{matrix}BH||CD\\BH=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH||CN\\BH=CN\end{matrix}\right.\) \(\Rightarrow BHNC\) là hình bình hành
\(\Rightarrow HN||BC\)
Chứng minh tương tự ta có BMHC là hình bình hành
\(\Rightarrow HM||BC\)
\(\Rightarrow H,M,N\) thẳng hàng