Cho tam giác ABC có 3 góc A nhọn và AB<AC.Tia phân giác của góc A cắt đường trung trực của đoạn BC tại I.Từ I vẽ IM vuông góc với AB và IN vuông góc với AC.Trên tia đối của tia CA lấy điểm E sao cho CE=AB(VẼ HÌNH GIÚP EM Ạ)
a)CM NC=BM
b)CM IN là đường trung trực của AE
c)Gọi F là giao điểm của BC và AI.Chứng minh FC>FB
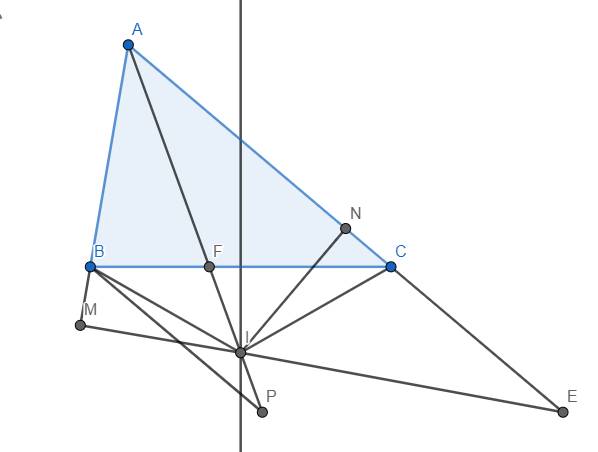
a) Do I nằm trên trung trực của đoạn BC nên \(IB=IC\).
Xét 2 tam giác IAM vuông tại M và IAN vuông tại N, ta có:
AI là cạnh chung và \(\widehat{MAI}=\widehat{NAI}\) (do AI là phân giác góc BAC)
\(\Rightarrow\Delta IAM=\Delta IAN\left(ch-gn\right)\) \(\Rightarrow IM=IN\).
Lại xét 2 tam giác IMB vuông tại M và INC vuông tại N, có:
\(IB=IC\left(cmt\right);IM=IN\left(cmt\right)\)
\(\Rightarrow\Delta IMB=\Delta INC\left(ch-cgv\right)\) \(\Rightarrow MB=NC\left(đpcm\right)\)
b) Ta đã có \(IN\perp AE\) tại N nên ta chỉ cần chứng minh N là trung điểm của đoạn AE là xong. Thật vậy, ta có \(MB=NC\left(cmt\right)\) và \(AB=EC\left(gt\right)\) nên suy ra \(AB+MB=NC+EC\) hay \(AM=NE\).
Mặt khác, do \(\Delta IAM=\Delta IAN\left(cmt\right)\Rightarrow AM=AN\)
Từ đó suy ra \(AN=NE\) hay N là trung điểm AE. Ta có đpcm.
c) Qua B kẻ đường thẳng song song với AC cắt AI tại P. Khi đó ta có \(\widehat{BAP}=\widehat{CAP}=\widehat{BPA}\) nên tam giác ABP cân tại B, suy ra \(AB=BP\). Mặt khác, theo định lý Thales, ta có \(\dfrac{FB}{FC}=\dfrac{BP}{AC}=\dfrac{AB}{AC}< 1\) (do \(AB< AC\)) nên suy ra \(\dfrac{FB}{FC}< 1\) hay \(FB< FC\) (đpcm)












