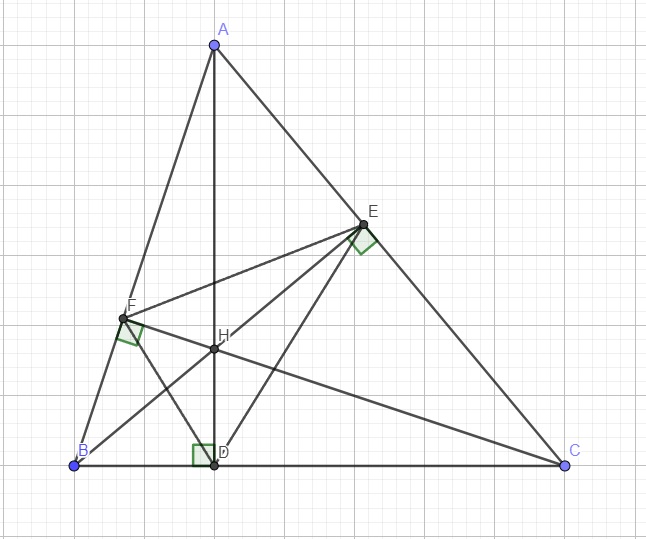
Cho tam giác ABC có 2 đường cao AD và BE cắt nhau tại H. Biết 3 góc CAB, ABC, BCA, đều là góc nhọn. Gọi F là giao điểm của CH và AB.
a) Chứng minh tứ giác CDHE là tứ giác nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác CDHE.
b) Chứng minh EBF = ECF.
c) Tìm tâm của đường tròn nội tiếp tam giác DEF
mn giúp e câu c trình bảy chi tiết với ạ
c.
Do CDHE nội tiếp \(\Rightarrow\widehat{ECH}=\widehat{EDH}\) (cùng chắn EH) hay \(\widehat{EDH}=\widehat{ECF}\)
Kết hợp câu b \(\Rightarrow\widehat{EBF}=\widehat{EDH}\) (1)
D và F cùng nhìn BH dưới 1 góc vuông \(\Rightarrow BDHF\) nội tiếp
\(\Rightarrow\widehat{FDH}=\widehat{FBH}\) (cùng chắn FH) hay \(\widehat{FDH}=\widehat{EBF}\) (2)
Từ (1);(2) \(\Rightarrow\widehat{EDH}=\widehat{FDH}\)
\(\Rightarrow DH\) là phân giác của \(\widehat{EDF}\)
Chứng minh tương tự ta có EH là phân giác của \(\widehat{DEF}\)
\(\Rightarrow H\) la giao điểm 2 đường phân giác trong của tam giác DEF
\(\Rightarrow H\) là tâm đường tròn nội tiếp tam giác DEF