Question

Cho tam giác ABC cân tại A.Trên cạnh AB,AC lần lượt lấy các điểm K,H sao cho AK=AH  . Gọi O là giao điểm của BH và CK . Chứng minh tam giác OBC cân

có vẽ hình nhé

Answer 1

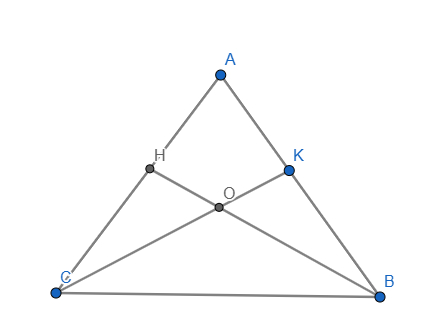
Vì \(\Delta\)ABC cân tại A \(\rightarrow AB=AC;\widehat{ABC}=\widehat{ACB}\)

Xét \(\Delta AHB\) và \(\Delta AKC\) có:

\(\widehat{A}\) chung

AH=AK (gt)

AB=AC

\(\rightarrow\Delta AHB=\Delta AKC\left(cgc\right)\)

\(\rightarrow\widehat{ABH}=\widehat{ACK}\) (2 góc tương ứng)

Ta có: \(\widehat{ABC}=\widehat{OBC}+\widehat{ABH}\); \(\widehat{ACB}=\widehat{OCB}+\widehat{ACK}\)

\(\widehat{ABC}+\widehat{ACB}\rightarrow\widehat{OBC}+\widehat{ABH}=\widehat{OCB}+\widehat{ACK}\)

mà \(\widehat{ABH}=\widehat{ACK}\)

\(\rightarrow\widehat{OBC}=\widehat{OCB}\)

\(\Rightarrow\Delta OBC\) cân tại O (đpcm)

 

Answer 2