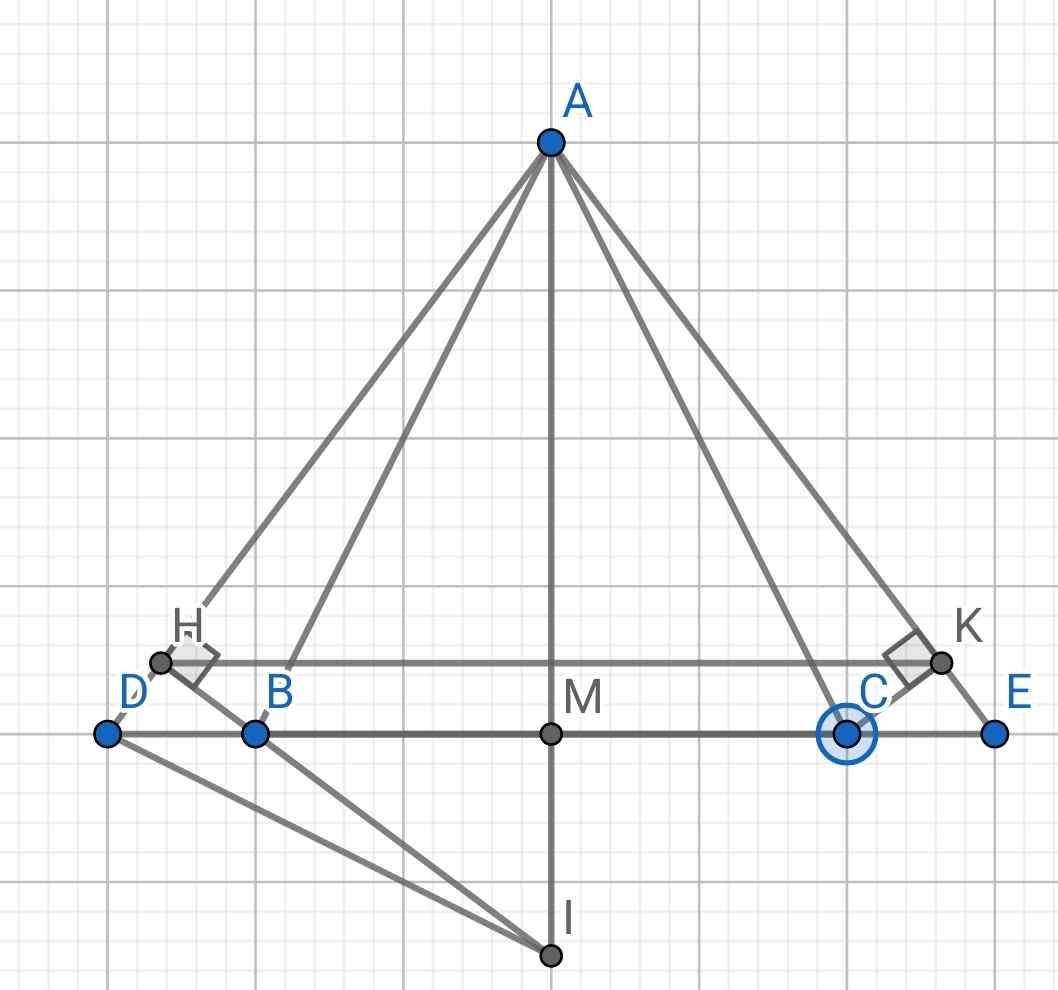
Cho tam giác abc cân tại a trung tuyến am trên tia đối tia bc lấy điểm d trên tia đối của cb lấy điểm e sao cho bd = ce a) chứng minh tam giác aed cân tại a b) chứng minh am là tia phân giác của dae c) từ b và c hạ bh , ck theo thứ tự vuông góc với ad và ae ( h thuộc ad , k thuộc ae ) chứng minh tam giác ahb = tam giác akc d) chứng minh hk // de e) gọi i là giao điểm của hb và am . Chứng minh ab vuông góc id
a: Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC tại M
=>AM\(\perp\)DE tại M
Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}=\widehat{CAK}\)(ΔABD=ΔACE)
Do đó: ΔAHB=ΔAKC
d: Xét ΔADI có
DM,IH là các đường cao
DM cắt IH tại B
Do đó: B là trực tâm của ΔADI
=>AB\(\perp\)DI