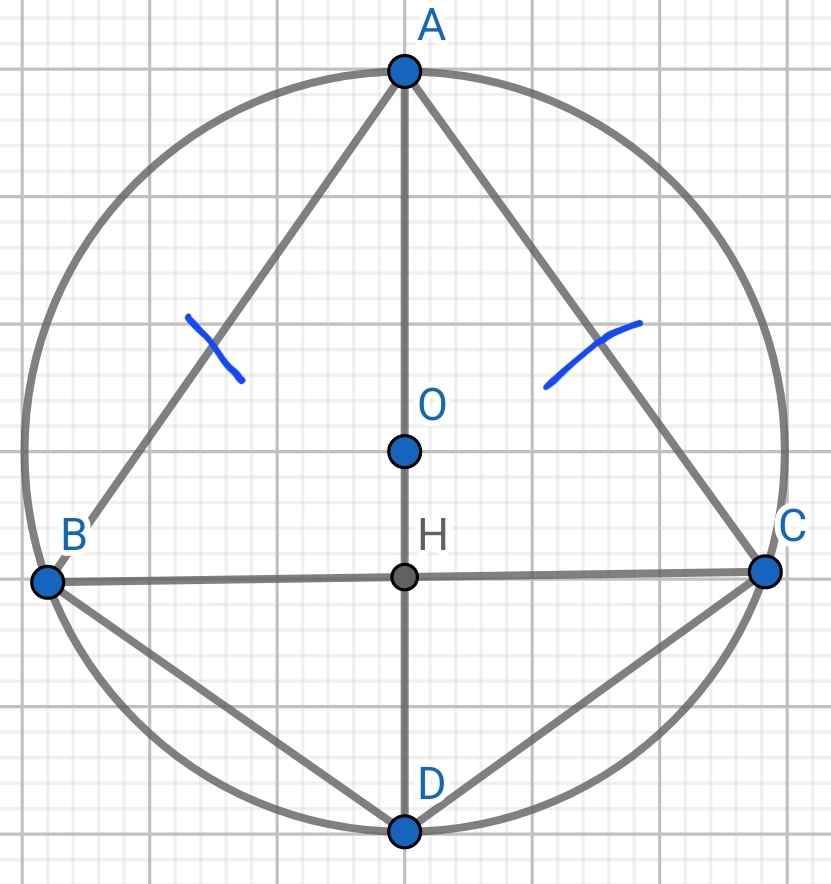
Do (O) là đường tròn ngoại tiếp ∆ABC
⇒ O là giao điểm của ba đường trung trực của ∆ABC
⇒ AO là đường trung trực của ∆ABC
⇒ AO ⊥ BC tại H
⇒ H là trung điểm BC
⇒ BH = BC : 2 = 12 : 2 = 6 (cm)
Do ∠ABD là góc nội tiếp chắn nửa đường tròn
⇒ ∠ABD = 90⁰
∆ABD vuông tại B có BH là đường cao
⇒ 1/BH² = 1/AB² + 1/BD²
⇒ 1/BD² = 1/BH² - 1/AB²
= 1/36 - 1/100
= 4/225
⇒ BD² = 225/4
⇒ BD = 15/2 = 7,5 (cm)
∆ABD vuông tại B
⇒ AD² = AB² + BD² (Pytago)
= 10² + 7,5²
= 156,25
⇒ AD = 12,5 (cm)
Để tính độ dài đoạn thẳng AD, ta cần tìm được tọa độ của điểm D trên đường tròn (O).
Gọi M là trung điểm của đoạn BC. Ta có AM là đường trung trực của BC, do đó OM vuông góc với BC và OM = MC = 6(cm).
Vì tam giác ABC cân tại A nên đường trung trực của BC cũng là đường cao của tam giác. Do đó, ta có AH là đường cao của tam giác ABC và AH = $\sqrt{AB^2 - BM^2}$ = $\sqrt{100 - 36}$ = $\sqrt{64}$ = 8(cm).
Ta có thể tính được AO bằng định lý Pythagoras trong tam giác vuông AOM:
$AO^2 = AM^2 + OM^2 = 10^2 - 6^2 + 6^2 = 100$
Vậy $AO = 10$ (cm).
Do đó, ta có thể tính được bán kính đường tròn (O) là $R = \frac{BC}{2} = 6$ (cm).
Gọi E là điểm đối xứng của A qua đường tròn (O). Ta có AE là đường đối xứng của AH qua đường tròn (O), do đó AE = AH = 8 (cm).
Ta có thể tính được độ dài đoạn thẳng DE bằng định lý Pythagoras trong tam giác vuông AOD:
$DE^2 = DO^2 + OE^2 = R^2 + AE^2 = 6^2 + 8^2 = 100$
Vậy $DE = 10$ (cm).
Ta cần tính độ dài đoạn thẳng AD. Ta có thể tính được độ dài đoạn thẳng HD bằng định lý Euclid:
$\frac{HD}{BD} = \frac{AH}{AB}$
$\Rightarrow HD = \frac{AH \cdot BD}{AB} = \frac{8 \cdot 6}{10} = \frac{24}{5}$ (cm)
Ta có thể tính được độ dài đoạn thẳng AO bằng định lý Pythagoras trong tam giác vuông AHO:
$AD^2 = AO^2 + OD^2 - 2 \cdot AO \cdot OD \cdot \cos{\angle AOD}$
Vì tam giác AOD cân tại O nên $\angle AOD = \frac{1}{2} \cdot \angle AOB$. Ta có thể tính được $\angle AOB$ bằng định lý cosin trong tam giác ABC:
$\cos{\angle AOB} = \frac{AB^2 + AC^2 - BC^2}{2 \cdot AB \cdot AC













