Sửa đề: \(\Delta ABC\) vuông tại A
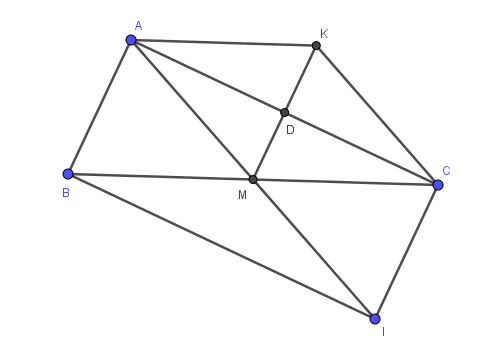
a) Do A đối xứng với I qua M (gt)
\(\Rightarrow M\) trung điểm của AI
Do AM là đường trung tuyến của \(\Delta ABC\left(gt\right)\)
\(\Rightarrow M\) là trung điểm của BC
Do \(\Delta ABC\) vuông tại A (gt)
\(\Rightarrow\widehat{BAC}=90^0\)
Tứ giác \(ABIC\) có:
M là trung điểm AI (cmt)
M là trung điểm của BC (cmt)
\(\Rightarrow ABIC\) là hình bình hành
Mà \(\widehat{BAC}=90^0\) (cmt)
\(\Rightarrow ABIC\) là hình chữ nhật
b) Do ABIC là hình chữ nhật
\(\Rightarrow AI=BC\) (hai đường chéo của hình chữ nhật)
\(\Rightarrow MA=MC\)
\(\Rightarrow\Delta MAC\) cân tại M
Gọi D là giao điểm của MK và AC
Do M và K đối xứng qua AC (gt)
\(\Rightarrow MK\perp AC\) và \(D\) là trung điểm của MK
\(\Rightarrow MD\perp AC\)
Mà \(\Delta MAC\) cân tại M
\(\Rightarrow MD\) vừa là đường cao, vừa là đường trung tuyến của \(\Delta MAC\)
\(\Rightarrow D\) là trung điểm của AC
Tứ giác AMCK có:
D là trung điểm của MK (cmt)
D là trung điểm của AC (cmt)
\(\Rightarrow AMCK\) là hình bình hành
Mà \(MK\perp AC\)
\(\Rightarrow AMCK\) là hình thoi













