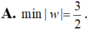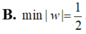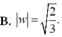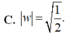\(\left(1+2i\right)z-5+3i=2+7i\)
=>\(z\left(1+2i\right)=2+7i-3i+5=4i+7\)
=>\(z=\dfrac{4i+7}{2i+1}=\dfrac{\left(4i+7\right)\left(2i-1\right)}{4i^2-1}=\dfrac{8i^2+10i-7}{-5}\)
\(=\dfrac{10i-15}{-5}=-2i+3\)
\(w=\dfrac{2z+3}{1-z}=\dfrac{2\left(-2i+3\right)}{1-\left(-2i+3\right)}=\dfrac{-4i+6}{1+2i-3}\)
\(=\dfrac{-4i+6}{2i-2}=\dfrac{-2i+3}{i-1}=\dfrac{\left(-2i+3\right)\left(i+1\right)}{i^2-1}\)
\(=\dfrac{-2i^2+i+3}{-2}=\dfrac{i+5}{-2}=\dfrac{-1}{2}i-\dfrac{5}{2}\)
\(\left|w\right|=\sqrt{\left(-\dfrac{1}{2}\right)^2+\left(-\dfrac{5}{2}\right)^2}=\sqrt{\dfrac{26}{4}}=\dfrac{\sqrt{26}}{2}\)
Đúng 0
Bình luận (1)
