Các câu hỏi tương tự
Cho số phức z, biết rằng các điểm biễu diễn hình học của các số phức z, iz và z+iz tạo thành một tam giác có diện tích bằng 18. Modun của số phức bằng A.
2
3
B.
3
2
C. 6 D. 9
Đọc tiếp
Cho số phức z, biết rằng các điểm biễu diễn hình học của các số phức z, iz và z+iz tạo thành một tam giác có diện tích bằng 18. Modun của số phức bằng
A. 2 3
B. 3 2
C. 6
D. 9
Trong các số phức thỏa mãn điều kiện
1
+
i
1
-
i
z
+
2
1
. Modun lớn nhất của số phức z bằng: A. 1 B. 4 C.
10
D. 3
Đọc tiếp
Trong các số phức thỏa mãn điều kiện 1 + i 1 - i z + 2 = 1 . Modun lớn nhất của số phức z bằng:
A. 1
B. 4
C. 10
D. 3
Cho số phức z thỏa mãn tập hợp |z-1|3. Biết rằng tập hợp các điểm biểu diễn số phức w với
3
−
2
i
w
i
z
+
2
là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó. A.
I
8
13
;
1
13...
Đọc tiếp
Cho số phức z thỏa mãn tập hợp |z-1|=3. Biết rằng tập hợp các điểm biểu diễn số phức w với 3 − 2 i w = i z + 2 là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó.
A. I 8 13 ; 1 13 , r = 3 13
B. I − 2 ; 3 , r = 13
C. I 4 13 ; 7 13 , r = 3 13
D. I 2 3 ; − 1 2 , r = 3
Cho số phức z thỏa mãn tập hợp |z-1|3. Biết rằng tập hợp các điểm biểu diễn số phức w với
3
−
2
i
w
i
z
+
2
là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó. A.
I
8
13
;
1
13...
Đọc tiếp
Cho số phức z thỏa mãn tập hợp |z-1|=3. Biết rằng tập hợp các điểm biểu diễn số phức w với 3 − 2 i w = i z + 2 là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó.
A. I 8 13 ; 1 13 , r = 3 13
B. I − 2 ; 3 , r = 13
C. I 4 13 ; 7 13 , r = 3 13
D. I 2 3 ; − 1 2 , r = 3
Biết số phức z thỏa mãn điều kiện
3
≤
z
−
3
i
+
1
≤
5
. Tập hợp các điểm biểu diễn của z tạo thành một hình phẳng. Diện tích của hình phẳng đó bằng A.
16
π
B.
4
π
C.
9
π
D.
25
π
Đọc tiếp
Biết số phức z thỏa mãn điều kiện 3 ≤ z − 3 i + 1 ≤ 5 . Tập hợp các điểm biểu diễn của z tạo thành một hình phẳng. Diện tích của hình phẳng đó bằng
A. 16 π
B. 4 π
C. 9 π
D. 25 π
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z. Tính
z
biết diện tích tam giác OAB bằng 8. A.
z
2
2
B.
z
4
2
C.
z...
Đọc tiếp
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và (1+i)z.
Tính z biết diện tích tam giác OAB bằng 8.
A. z = 2 2
B. z = 4 2
C. z = 2
D. z = 4
Cho số phức z thỏa mãn
i
z
-
-
3
+
i
2
Trong mặt phẳng phức, đồ thị nào hiển thị đúng quỹ tích điểm biểu diễ hình học của số phức z.
Đọc tiếp
Cho số phức z thỏa mãn i z - - 3 + i = 2 Trong mặt phẳng phức, đồ thị nào hiển thị đúng quỹ tích điểm biểu diễ hình học của số phức z.
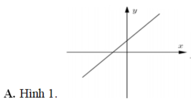
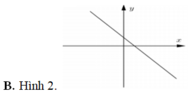
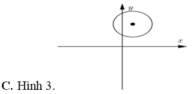
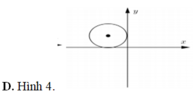
Cho số phức z x + yi. Tập hợp các điểm biểu diễn của số phức z sao cho số phức
z
+
i
z
-
i
là một số thực âm là: A. Các điểm trên trục hoành với -1x1 B. Các điểm trên trục tung với -1y1 C. Các điểm trên trục tung với
-
1
≤
y
1
D. Các điểm trên trục tung với ...
Đọc tiếp
Cho số phức z = x + yi. Tập hợp các điểm biểu diễn của số phức z sao cho số phức z + i z - i là một số thực âm là:
A. Các điểm trên trục hoành với -1<x<1
B. Các điểm trên trục tung với -1<y<1
C. Các điểm trên trục tung với - 1 ≤ y < 1
D. Các điểm trên trục tung với y ≤ - 1 y ≥ 1
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và
i
+
1
z
. Tính z biết diện tích tam giác OAB bằng 8.
Đọc tiếp
Cho số phức z. Gọi A, B lần lượt là các điểm trong mặt phẳng Oxy biểu diễn các số phức z và i + 1 z . Tính z biết diện tích tam giác OAB bằng 8.
![]()
![]()
![]()
![]()



