Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:

Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:

Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tính mô đun của số phức w = z ¯ + i z
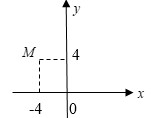
A. w = 12
B. w = 28
C. w = 182
D. w = 128
Cho số phức z thỏa z + 2 + i z - = 3 + 5 i .Tính mô đun của số phức z -
A. z = 13
B. z = 5
C. |z|=13
D. |z|=5
Cho số phức z thỏa mãn z = 1 - 3 i 3 1 - i . Tìm mô đun của số phức z + i z
A. 8
B. -8
C. 8 2
D. 16
Cho số phức z=a+bi. Mô đun của số phức z bằng:
A. a 2 - b 2
B. a 2 + b 2
C. a 2 + b 2
D. a 2 - b 2
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z ¯ = - 7 + 3 i + z . Mô đun của số phức w = 1 - z - z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Cho số phức z = (2+i)(1-i) + 1 +2i. Mô-đun của số phức z là
A. 2 2
B. 4 2
C. 17
D. 2 5
Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z = a + bi (a, b Î R, ab ¹ 0 ), M' là điểm biểu diễn cho số phức z → . Mệnh đề nào sau đây đúng?
A. M' đối xứng với M qua Oy
B. M' đối xứng với M qua Ox
C. M' đối xứng với M qua đường thẳng y = x.
D. M' đối xứng với M qua O
Cho số phức z = x + y i x , y ∈ ℝ . Tập hợp các điểm biểu diễn của số phức z sao cho số phức z + i z - i là một số thực âm là:
A. Các điểm trên trục hoành với -1 < x < 1
B. Các điểm trên trục tung với -1 < y < 1
C. Các điểm trên trục tung với - 1 ≤ y < 1
D. Các điểm trên trục tung với | y ≥ 1 y ≤ - 1
Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức z’ với z ' = - 3 - 2 i . Tìm mệnh đề đúng trong các mệnh đề sau
A. Hai điểm A và B đối xứng nhau qua trục hoành
B. Hai điểm A và B đối xứng nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x