Các câu hỏi tương tự
Cho số phức za+bi, a,bÎR. Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng y -2 và y 2 như hình vẽ bên thì điều kiện của a và b là: A.
-
2
≤
a
≤
2
b
∈
R
B. ...
Đọc tiếp
Cho số phức z=a+bi, a,bÎR. Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng y = -2 và y = 2 như hình vẽ bên thì điều kiện của a và b là:
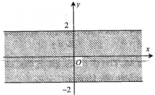
A. - 2 ≤ a ≤ 2 b ∈ R
B. a ≤ 2 b ≥ - 2
C. - 2 ≤ a ≤ 2 - 2 ≤ b ≤ 2
D. a ∈ R - 2 ≤ b ≤ 2
Cho số phức
z
a
+
b
i
,
a
,
b
∈
R
. Tìm điều kiện của a và b để điểm biểu diễn của z thuộc dải giới hạn bởi đường thẳng
x
-
2
và
x
2
như hình vẽ bên A.
a
≥
2
b...
Đọc tiếp
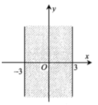
Cho số phức z = a + b i , a , b ∈ R . Tìm điều kiện của a và b để điểm biểu diễn của z thuộc dải giới hạn bởi đường thẳng x = - 2 và x = 2 như hình vẽ bên
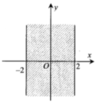
A. a ≥ 2 b ≥ 2
B. a ≤ 2 b ≤ - 2
C. a ≤ 2 b ≥ - 2
D. - 2 ≤ a ≤ 2 b ∈ R
Cho số phức za+bi, a,bÎR. Điểm biểu diễn z thuộc dải giới hạn bởi hai đường thẳng y -5 và y 5 như hình vẽ bên. Tìm điều kiện của a và b. A.
-
5
≤
a
≤
5
-
5
≤
b
≤
5...
Đọc tiếp
Cho số phức z=a+bi, a,bÎR. Điểm biểu diễn z thuộc dải giới hạn bởi hai đường thẳng y = -5 và y = 5 như hình vẽ bên. Tìm điều kiện của a và b.
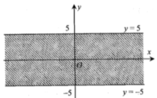
A. - 5 ≤ a ≤ 5 - 5 ≤ b ≤ 5
B. - 5 ≤ a ≤ 5 b ∈ R
C. a ∈ R - 5 ≤ b ≤ 5
D. a ≤ 5 b ≥ - 5
Cho số phức
z
a
+
b
i
,
a
,
b
∈
R
. Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc hình tròn tâm O bán kính R 2 như hình vẽ bên thì điều kiện của a và b là A.
-
2
≤
a
≤
2...
Đọc tiếp
Cho số phức z = a + b i , a , b ∈ R . Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc hình tròn tâm O bán kính R = 2 như hình vẽ bên thì điều kiện của a và b là
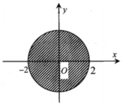
A. - 2 ≤ a ≤ 2 - 2 ≤ b ≤ 2
B. a 2 + b 2 ≤ 4
C. a 2 + b 2 > 4
D. a < - 2 ; b > 2
Cho số phức za+bi, a,b ÎR. Tìm điều kiện của a và b để điểm biểu diễn z thuộc hình tròn tâm O bán kính R 3 như hình vẽ bên A.
a
2
+
b
2
9
B.
-
3
≤
a
≤
3
-
3...
Đọc tiếp
Cho số phức z=a+bi, a,b ÎR. Tìm điều kiện của a và b để điểm biểu diễn z thuộc hình tròn tâm O bán kính R = 3 như hình vẽ bên
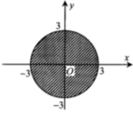
A. a 2 + b 2 > 9
B. - 3 ≤ a ≤ 3 - 3 ≤ b ≤ 3
C. a 2 + b 2 ≤ 9
D. a < - 3 b > 3
Trong mặt phẳng tọa độ như hình bên, số phức
z
3
-
4
i
được biểu diễn bởi điểm nào trong các điểm A, B, C, D? A. Điểm A B. Điểm B C. Điểm C D. Điểm D
Đọc tiếp
Trong mặt phẳng tọa độ như hình bên, số phức z = 3 - 4 i được biểu diễn bởi điểm nào trong các điểm A, B, C, D?
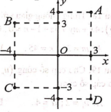
A. Điểm A
B. Điểm B
C. Điểm C
D. Điểm D
Cho hai số phức
z
a
+
bi
;
a
,
b
∈
ℝ
. Có điểm biểu diễn của số phức z nằm trong dải
−
2
;
2
(hình 1) điều kiện của a và b là: ...
Đọc tiếp
Cho hai số phức z = a + bi ; a , b ∈ ℝ . Có điểm biểu diễn của số phức z nằm trong dải − 2 ; 2 (hình 1) điều kiện của a và b là: a ≥ 2 b ≥ 2 a ≤ − 2 b ≤ − 2 − 2 < a < 2 , b ∈ ℝ a , b ∈ − 2 ; 2
A. a ≥ 2 b ≥ 2
B. a ≤ − 2 b ≤ − 2
C. − 2 < a < 2 , b ∈ ℝ
D. a , b ∈ − 2 ; 2
Trong mặt phẳng tọa độ cho hai điểm A(4;0) và B(0;-3). Điểm C thỏa mãn điều kiện
O
C
⇀
O
A
⇀
+
O
B
⇀
. Khi đó, số phức biểu diễn bởi điểm C là: A. z4-3i B. z4+3i C. z-3-4i D. z-3+4i
Đọc tiếp
Trong mặt phẳng tọa độ cho hai điểm A(4;0) và B(0;-3). Điểm C thỏa mãn điều kiện O C ⇀ = O A ⇀ + O B ⇀ . Khi đó, số phức biểu diễn bởi điểm C là:
A. z=4-3i
B. z=4+3i
C. z=-3-4i
D. z=-3+4i
Gọi A là điểm biểu diễn của số phức
z
2
+
3
i
và B là điểm biểu diễn của số phức
z
’
3
+
2
i
trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng? A. Hai điểm A và B đối xứng nhau qua đường thẳng yx B. Hai điểm A và B đối xứng nhau qua trục tung C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O D. Hai điểm A và B đối xứng nhau qua trục hoành
Đọc tiếp
Gọi A là điểm biểu diễn của số phức z = 2 + 3 i và B là điểm biểu diễn của số phức z ’ = 3 + 2 i trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
A. Hai điểm A và B đối xứng nhau qua đường thẳng y=x
B. Hai điểm A và B đối xứng nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng nhau qua trục hoành