Các câu hỏi tương tự
Cho số phức
z
a
+
a
2
i
, aÎR. Khi đó điểm biểu diễn của số phức liên hợp của z trên mặt phẳng tọa độ nằm trên đồ thị hàm số A.
y
-
x
B.
y
-
x
2
C.
y
x
2
D.
y
x
Đọc tiếp
Cho số phức z = a + a 2 i , aÎR. Khi đó điểm biểu diễn của số phức liên hợp của z trên mặt phẳng tọa độ nằm trên đồ thị hàm số
A. y = - x
B. y = - x 2
C. y = x 2
D. y = x
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
cho hàm số y = a/x ; a) xác định hệ số a biết đồ thị của nó đi qua điểm (-2;2) , b) vẽ đò thị hàm số đó và đường thẳng y = 2 trên cùng 1 hệ trục tọa độ Oxy ( đồ thị hàm số là đường cong hypebol) c) dựa vào đồ thị để tìm các giá trị của x sao cho 1/x<-2
Đường thẳng x k cắt đồ thị hàm số
y
log
5
x
và đồ thị hàm số
y
log
3
(
x
+
4
)
. Khoảng cách giữa các giao điểm là 1/2. Biết
k
a
+
b
,
trong đó a, b là các số nguyên. Khi đó tổng a + b bằng A. 7 B. 6 C. 8 D. 5
Đọc tiếp
Đường thẳng x = k cắt đồ thị hàm số y = log 5 x và đồ thị hàm số y = log 3 ( x + 4 ) . Khoảng cách giữa các giao điểm là 1/2. Biết k = a + b , trong đó a, b là các số nguyên. Khi đó tổng a + b bằng
A. 7
B. 6
C. 8
D. 5
Cho hàm số
y
x
+
b
a
x
-
2
a
b
≠
-
2
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng
d
:
3
x
+
y...
Đọc tiếp
Cho hàm số y = x + b a x - 2 a b ≠ - 2 . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng d : 3 x + y - 4 = 0 . Khi đó giá trị của a - 3b bằng
A. -2
B. 4
C. -1
D. 5
Cho hàm số
y
x
+
b
a
x
-
2
a
b
≠
-
2
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng
d
:
3
x
+...
Đọc tiếp
Cho hàm số y = x + b a x - 2 a b ≠ - 2 . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-2) song song với đường thẳng d : 3 x + y - 4 = 0 . Khi đó giá trị của a - 3 b bằng
A. -2
B. 4
C. -1
D. 5
Cho (C) là đồ thị của hàm số
y
x
-
2
x
+
1
và đường thẳng
d
:
y
m
x
+
1
. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A.
m
≥
0...
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 và đường thẳng d : y = m x + 1 . Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A. m ≥ 0
B. m < 0
C. m ≤ 0
D. m > 0
Cho hàm số yf(x) xác định, liên tục trên tập R{1} và có bảng biến thiênSố mệnh đề đúng trong các mệnh đề sau là? 1. Đường thẳng y2 là đường tiệm cận ngang của đồ thị hàm số. 2. Đường thẳng x1 là đường tiệm cận đứng của đồ thị hàm số. 3. Hàm số đồng biến trên các khoảng
-
∞
;
1
và
1
;
+
∞
A. 0. B....
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên
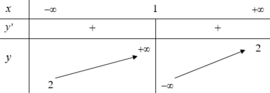
Số mệnh đề đúng trong các mệnh đề sau là?
1. Đường thẳng y=2 là đường tiệm cận ngang của đồ thị hàm số.
2. Đường thẳng x=1 là đường tiệm cận đứng của đồ thị hàm số.
3. Hàm số đồng biến trên các khoảng - ∞ ; 1 và 1 ; + ∞
A. 0.
B. 1
C. 2.
D. 3




